데이터사이언스

카테고리 없음

_금융덕후_ 2021. 1. 30. 23:56

728x90

분포 (distribution)

분포란 데이터의 값이 어떠한 형태로 퍼져 있는지에 대한 정보이다.

표본 분포란 모집단에서 얻은 샘플 데이터가 나타내는 형태에 대한 정보이다.

좋은 표본의 분포는 모집단의 분포를 크게 반영한다.

중심극한정리는 표본의 크기가 커질 수록 표본분포는 정규분포를 따르는 경향이 있다는 이론이다.

모집단이 정규분포가 아니더라도, 표본의 크기가 충분하다면 정규분포를 따른다고 가정한다.

신뢰구간이란 모수가 실제로 포함될 것으로 예측되는 범위이다.

보통 신뢰구간은 어떠한 큰 수치(예, 95% 혹은 90%)로 표현이 된다.

정규분포의 90%의 신뢰 구간을 따른다고 하면,

중심(평균)으로부터 위 아래 90%가 모수에 포함될 것으로 강하게 예측된다는 의미이다.

몇가지 대표적인 분포들을 알아본다.

가장 기본적이며 가장 많이 사용되는 분포이다.

평균이 중앙에 있고, 표준편차만큼 서서히 감소하는 모양을 띈다.

실제 데이터들의 표본은 정규분포를 잘 따르지 않지만,

통계적으로 다루기 쉬운 분포이기 때문에 많은 통계정 추론의 가정을 정규분포로 하게 된다.

평균이 0, 표준편차가 1인 분포를 표준정규분포 (standard normal distribution) 이라고 한다.

분포를 표준정규분포로 만들어 주면 평균에서의 거리가 기존과는 다르게 된다..

z스코어란 이 변화의 정도를 측정하는 수치로,

평균값에서 표준편차의 몇배 정도가 떨어져 있다는 것을 평가하는 수치이다.

$z = \frac{x - \mu}{\sigma}

예/아니오 등 이진의 결과를 얻는 과정에서 나타나는 분포이다.

독립적인 결과를 가져오는 시행(trial)을 통해 결과를 도출하는데,

두가지 결과는 합해서 1이 되는 확률을 가진다.

이 때 확률은 꼭 50대 50일 필요는 없다.

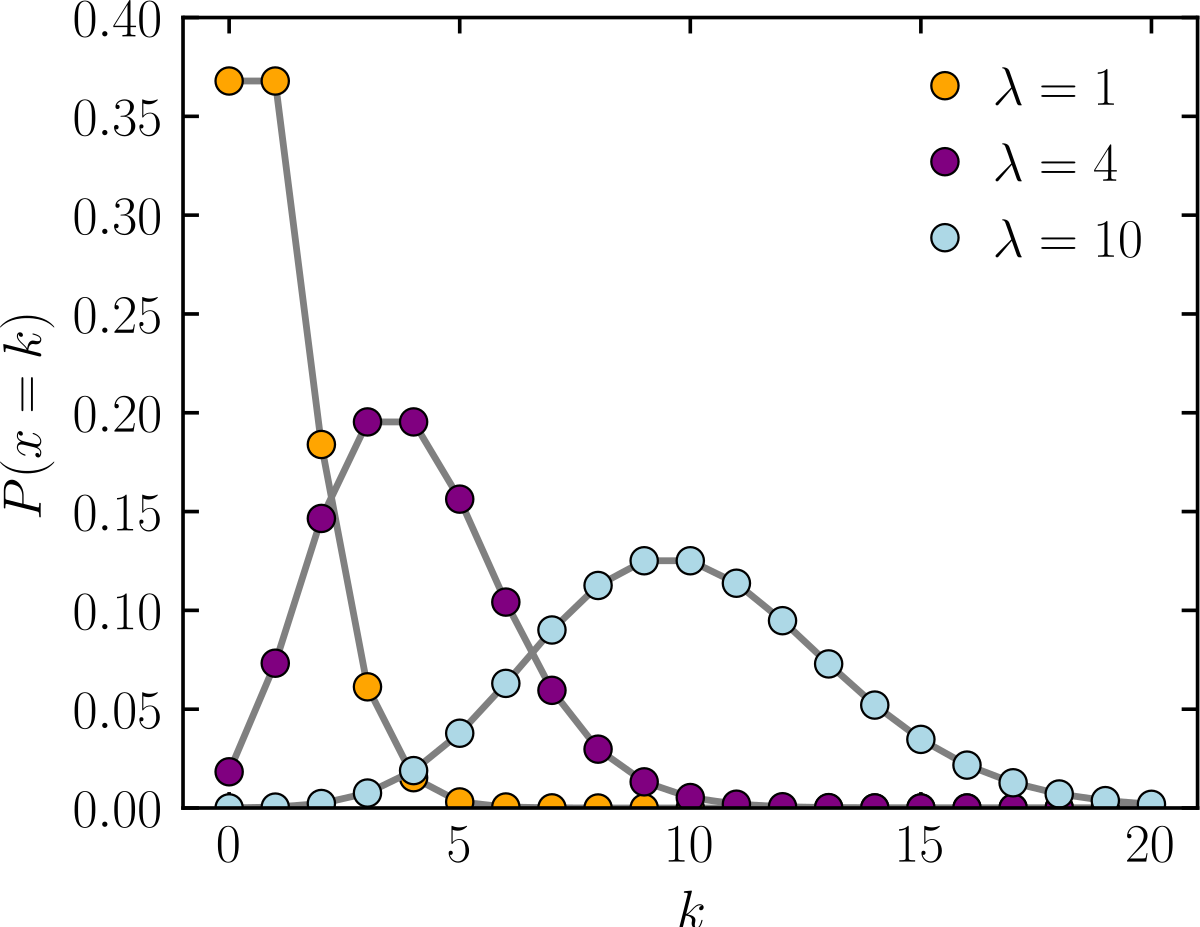
이산의 확률 분포의 일종으로, 미리 정해놓은 단위시간과 단위공간 안에서,

한 사건이 몇번 발생할 것인가를 표현하는 확률분포이다.

푸아송분포는 람다($\lambda$)라는 매개 변수를 통해 단위시간/단위공간 안에서

한 사건이 발생할 평균적인 사건의 수를 설정한다.

이 사건의 수를 통계적 용어로는 기댓값(expectation)이라고도 한다.

따라서 이 람다값에 따라 사건이 발생할 확률이 샘플링 되는 분포가 변하게 된다.

728x90