
강화학습
정책 (Policy)
정책은 에이전트가 어떻게 행동을 선택하는지를 정의한다.
강화학습에서의 정책은 보통 $\pi$로 정의한다.
확정적 정책 (Deterministic Policy)

확정적 정책은 위 그림에서와 같이 각 상태당 정해진 행동이 존재한다.
보이는 바와 같이 에이전트는 각기 다른 상태에서 같은 행동을 선택할 수도 있고,
어떠한 행동은 아예 선택하지 않을 수도 있다.
$\pi(s) = a$
위 그림을 테이블로 표현하면 다음과 같이 표현 가능하다:
| State | Action |
| $s_0$ | $a_1$ |
| $s_1$| | $a_0$ |
| $s_2$ | $a_0$ |
예제)

에이전트가 집으로 가는 문제를 풀고있다고 하자.
에이전트는 상하좌우로 움직일 수 있고,
그림의 각 방향 화살표는 하나의 정책이 된다.
각 화살표는 각 상태(칸)에서 어떤 방향으로 움직여야하는지를 가르쳐준다.
확률적 정책 (Stochastic Policy)
확률적인 정책은 각 상태에서 각 행동을 취할 가능성을 확률로 표현한다.
이 가능성은 0과 1사이의 0이 아닌 어떤 확률 값이다.
$0 < \pi(a|s) \le 1$
또한 이 확률들은 확률의 성질에 따라 모두 더하면 1이 된다.
$\sum_{a \in A(s)} \pi(a|s) = 1$
위 예제에서의 상태 $s_0$에서와 $s_1$에서 정책을 다음과 같은 확률로 정의해볼 수 있다.

예제)

앞서 이야기한 집으로 가는 예제에서,
각 상태별 행동의 선택 확률을 다음과 같이 결정할 수도 있다.
아래줄의 첫 세 칸은 왼쪽이나 위쪽 모두 움직여도 집을 향해 가기 때문에,
두개의 행동 모두 같은 확률을 가질 수 있다.
확률적 정책은 현재 상태가 행동을 선택할 모든 정보를 가지고 있다고 가정한다.
MDP와 같이 이전 상태들과 미래를 고려한다는 가정하에서도,
이전에 선택했던 행동들의 결과가 현재 상태를 정의하기 때문에,
현재 상태만을 가지고 행동을 선택할 모든것이 주어졌다고 판단할 수 있는 것이다.
가치 (Value)
강화학습에서는 보상이 가장 가까운 시일의 결과를 표현한다.
다른말로 하면 현재 상태에서 선택한 행동의 결과는 바로 다음 상태에서 받는 보상이 정의한다.
하지만 강화학습은 장기적인 결과를 최대화 할수 있는 것을 목표로 한다.
이 장기적인 결과를 정의하는 것이 가치함수이다.
상태가치함수 (State-value function)
상태 가치함수는 에이전트가 어떠한 상태에서 시작했을 때 기대되는 미래의 결과를 정의한다.
이는 곧 에이전트가 현재 상태에서부터 얻을 수 있는, 예측되는 보상을 의미한다.
$v(s) \dot{=} \mathbb{E} [G_t | S_t = s]$
위 수식에서 $G_t$가 감가율이 적용된 전체의 보상임을 기억하자.
$G_t = \sum_{k=0}^\infty \gamma^k R_{t+k+1}$
정책에 의한 상태가치함수를 정의하면 다음과 같다:
$v_{\pi}(s) \dot{=} \mathbb{E}_{\pi} [G_t | S_t = s]$
가치함수의 $\pi$는 현재의 가치가 정책에 의해 선택되었음을 의미하고,
기댓값 $\mathbb{E}$의 $\pi$는 현재 정책을 따라 이동했을때의 가치를 의미한다.
행동가치함수 (Action-value function)
위와 동일하게 행동가치함수를 다시 정의하면 다음과 같다:
$q_{\pi}(s,a) \dot{=} \mathbb{E}_{\pi}[G_t | S_t = s, A_t = a]$
이는 현재 상태 $s$에서 행동 $a$를 선택한 뒤 정책 $\pi$를 따라 이동했을떄의 가치를 의미한다.
보상 예측
강화학습에서 가치함수는 매우 중요하다.

위 그림에 보이는 바와 같이 가치함수는
정책을 따라 현재 상태에서 출발했을 때 미래에 얻을 수 있는 보상을 예측한다.
이는 에이전트가 끝까지 가보지 않고, 미래를 예상함으로서 현재의 행동을 정의할 수 있게 한다.
현재의 보상과 미래의 예측불허의 동적인 일(unknown dynamics)들을 모두 고려해,
이를 평균적인 가치로 환산하는 것이다.
예제)
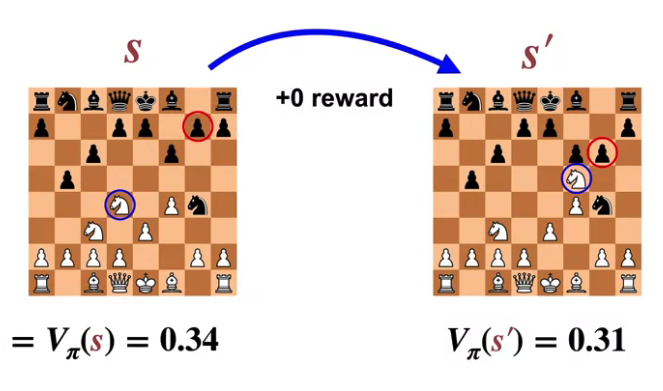
체스 게임을 예로 들어보자.
현재의 상태는 주어진 모든 말들과 상대방의 말들을 모두 고려한다.
주어진 보상은 게임을 이겼을 때 1 뿐이라면, 보상은 많은 것을 알려주지 않는다.
하지만 가치함수는 미래의 이 보상을 고려해 게임에서 이길 확률을 계산하게 된다.
$S$를 현재 상태 $S'$를 다음으로 선택 가능한 상태중 하나라고 가정한다면,
이를 가치로 환산했을때 현재는 0.34, 미래는 0.31이기 때문에,
에이전트는 이 행동을 선택하지 않게 될 것이다.
'데이터사이언스 > 강화학습' 카테고리의 다른 글
| 강화학습 - (10) 벨만 최적 방정식 (0) | 2020.09.17 |
|---|---|
| 강화학습 - (9) 벨만방정식 (0) | 2020.09.14 |
| 강화학습 - (7) 연속적인 결정과정 (0) | 2020.09.14 |
| 강화학습 - (6) 보상 (2) | 2020.09.07 |
| 강화학습 - (5) 마르코프 결정과정 (0) | 2020.09.06 |