추천시스템

본 포스팅은 Minnesota대학교의 Intro to Recommender Systems코세라 강좌를 정리한 내용입니다.
https://www.coursera.org/learn/collaborative-filtering?specialization=recommender-systems
잠재 의미 분석 (Latent Semantic Analysis)
- 정보검색 분야에서도 비슷한 고민을 먼저 시작했다.
- 문서의 키워드벡터와 쿼리의 키워드벡터 들의 조합은 간단하지만 좋은 표현법은 아니다. - 의미를 내포하기가 힘들다
- 이것을 해결하기 위해 특이값분해 (Singular Value Decomposition, SVD)라는 테크닉을 사용한다.
- SVD는 행렬을 사용자-아이템 행렬에서 선호도 기반의 작은 행렬로 감소시킨다.
Singular Value Decomposition, SVD
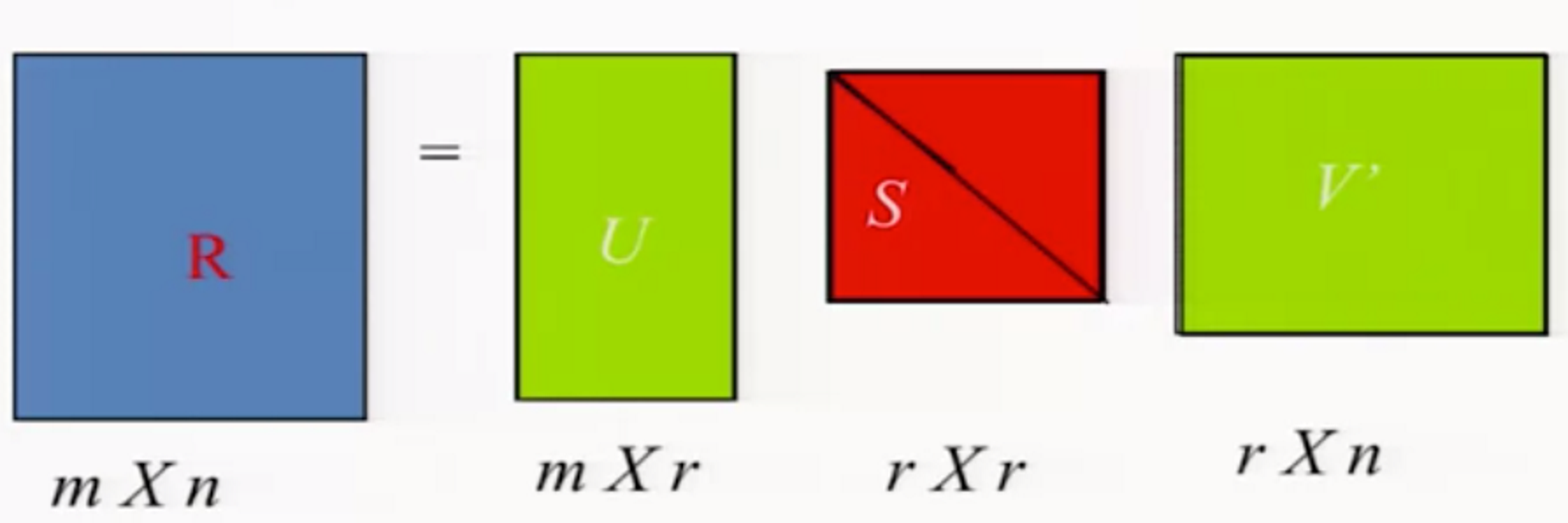
- 위의 그림 왼쪽에 랭크R의 행렬이 있다. (랭크는 행렬의 선형적으로 독립적인 행/열의 갯수를 의미한다. 독립적인 행이 3개면 랭크3)
- 행렬은 m명의 사용자와 n개의 아이템에 대한 평점이 기록되어 있다. (현재는 그 정보들이 모두 다 채워져 있다고 가정한다.)
- 위의 행렬은 두개의 랭크 R행렬로 분해가 가능하다 (U와 V')
- 그리고 그를 위해 대각행렬 S를 사용한다.
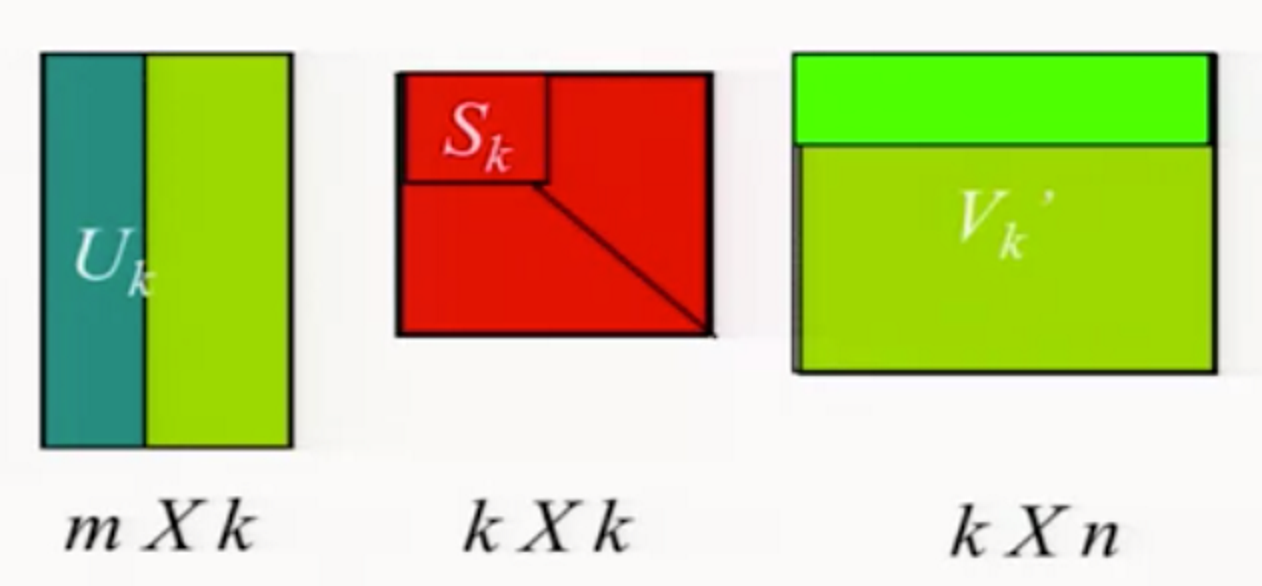
- 중요한점은, 대각행렬S의 값들의 절대값들이 각 디멘션의 중요도를 나타낸다는 것이다.
- 예를들어, S의 절대값들을 정렬하고 K만큼을 잘라냈다고 하자. 그렇다면 랭크 K의 행렬이 될것이다.
- 양쪽의 행렬들도 위 그림과 같이 k만큼 자른 뒤 다시 곱하면, K디멘션의 행렬이 나오게 된다.
- 이 새로나온 행렬이 곧 압축된 선호도공간이 된다.
협업필터링과 SVD
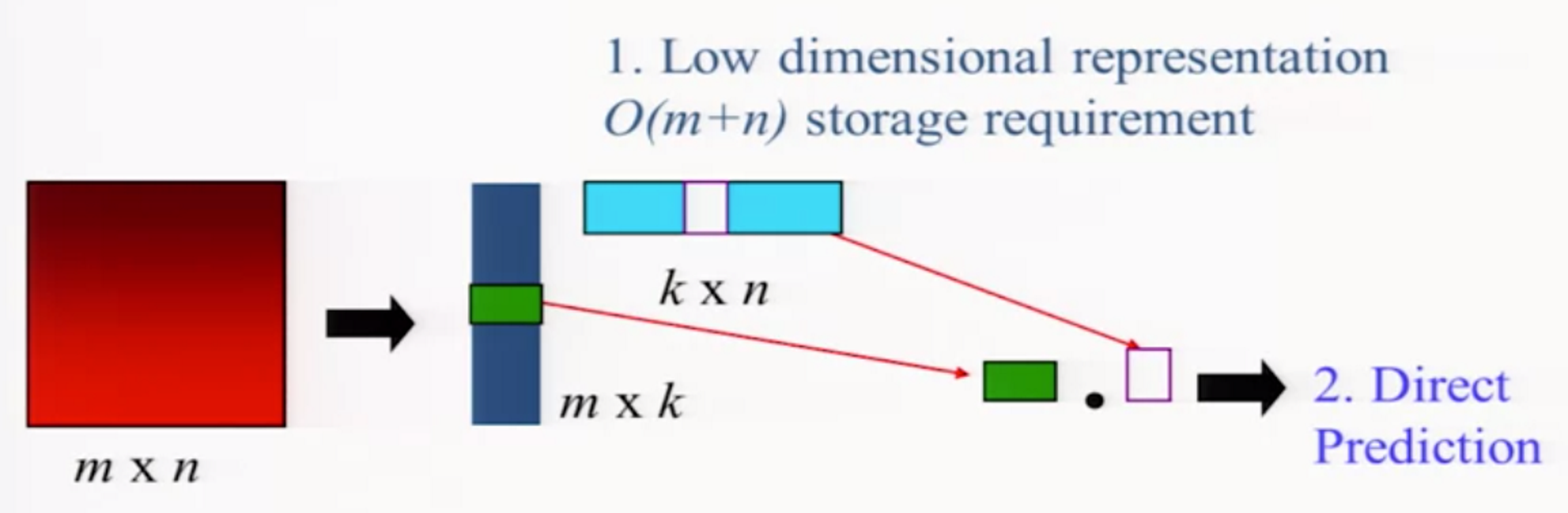
- 사용자들의 선호도를 k개의 원소를 가진 벡터로 표현하고 (네이비색)
- 각 아이템을 k개의 원소를 가진 벡터로 표현했다고 하자 (하늘색)
- 고른 벡터들을 내적곱을 하면 각 아이템에 대한 선호도를 구할 수 있다.
각 디멘션은 무엇인가?
- 각 디멘션은 사용자와 아이템에 대한 평점에서부터 오기 때문에, 컨텐츠기반필터링은 아니다. (각 디멘션이 아이템의 속성이 아니고 사용자의 선호도이기 때문이다.)
SVD의장점과 문제점
장점
- 디멘션을 줄여준다. (동의성문제와 계산복잡도를 줄여준다)
- 더 리치(rich)한 이웃네트워크를 형성해준다.
- 어떤 디멘션으로 줄일것인가는 실험에 의해 알아내야 한다. 보통은 (영화는 13~20개)
문제점들
- 평점 행렬에 빈 공간(정보)이 있다면 어떻게 해야하나?
- 계산 복잡도는 어떻게 되나? - 많이 복잡하긴 하다
- $O(m^2n + n^3)$
- 직접 수행하지 않고 더 효율적으로 예측하는 모델이 있다.
- 사람이 쉽게 이해할 수 없다 (설명이 불가능한다)
- 각 디멘션이 어떻게 선호도와 아이템의 관계가 되는가?
Singular Vector Decomposition 부가설명
$R = P \sum Q^{T}$
R은 m x n의 평점 행렬이다
P는 사용자 특성 행렬
- P의 각 행($\overrightarrow{p}_{u}$)은 한 사용자의 특성들에 대한 선호도를 말한다
Q는 아이템 특성 행렬
- Q의 각 행($\overrightarrow{q}_{i}$)은 각 특성에 대한 아이템의 연관성을 말한다.
$\sum$은 각 특성들의 중요도에대한 값을 가진 대각행렬이다
P와 Q는 서로가 직교행렬이다
행렬분해는 숫자를 분해하는 작업과 비슷하다.( 15를 분해하면 3과 5로 나뉘듯이 이 작업도 비슷하다는 의미)
SVD는 선호도를 잠재적인 특성들로 묘사한다. 그리고 그 특성들은 평점들로부터 "학습"된다. 이 특성들은 사용자들이 아이템들에 대해 가진 선호도를 "설명"하는 역할을 하는데, 대부분은 사람이 바로 해석할 수 없는 정보이다. (사용자들이 애니메이션 영화를 얼마나 좋아하는가?와 같은 특성이 아니라는 이야기이다.) 하지만 이 해석이 불가능한 특성들을 통해 잠재적으로 사용자들이 좋아할만한 특성을 찾아내는 것이다.
SVD는 사용자와 아이템들에 대한 공유된 벡터공간을 만들어내는데, 사용자 공간인 $\overrightarrow{r}_{u}$와 아이템 공간인 $\overrightarrow{r}_{i}$가 SVD로 형성된 $\overrightarrow{p}_{u}$와 $\overrightarrow{q}_{i}$로 표현이 되게 되는것이다.
평점 행렬과는 다르게 Factorization으로 만들어진 행렬은 dense하다. 평점행렬에서는 많은 값들이 0이었지만 (sparse) 이 새로운 행렬들은 값들이 모두 차있다.
예측법 (Prediction Rule)
위의 수식을 다시 표현하면 아래와 같은 예측 수식이 나온다.
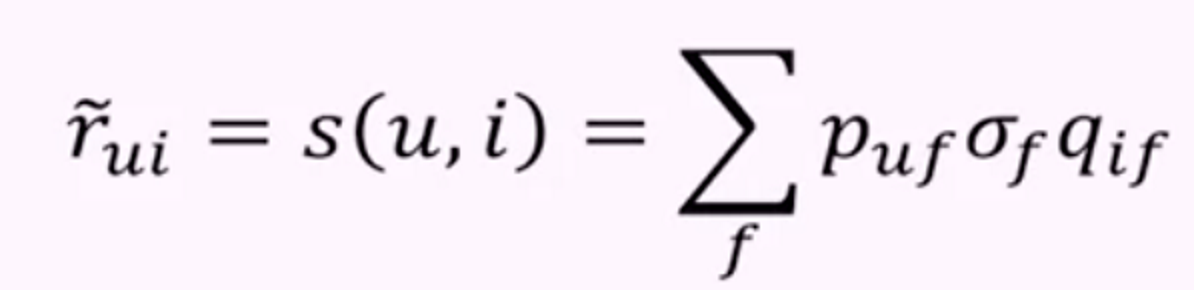
수식을 잘 보면, 벡터들을 모두 곱해 더하는 수식이기 때문에,
위의 R의 수식과 다르지 않은것을 알 수 있다.
간혹 SVD를 구할 때 baseline을 구하기도 한다:
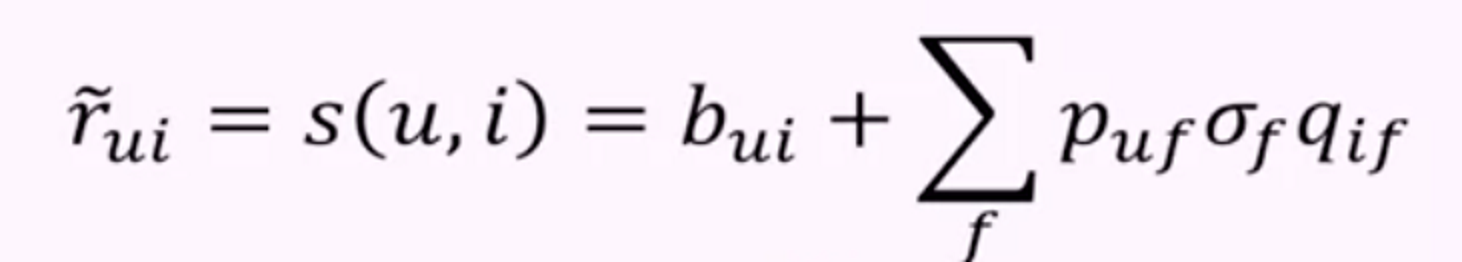
이 baseline은 모든 (존재하는)값의 평균값(global mean)으로 계산 된다.
비어있는 정보 채우기
SVD는 행렬의 모든 정보가 채워져 있어야 가능하다, 그렇다면 비어있는 정보들 (이전 예제들에서의 NaN값)은 어떻게 채워줄 수 있을까?
- 평균값으로 충당한다
- 평균값을 baseline으로 하고, 없는 값들을 0으로, 있는값들에서 baseline을 뺸값으로 할당한다.
- 무시한다 (추후에 설명)
새로운 데이터
현실의 시스템에선 사용자들의 데이터가 워낙 많기 때문에 계산하는데 시간이 많이 걸린다.
그렇다면 새로운 데이터가 들어오면 어떻게 처리해야 할까? Folding In이라는 방법이 있다.
먼저 기존에 사용하던 수식을 생각해보자:
$R = P \sum Q^{T}$
우리는 $\overrightarrow{r}_{u}$를 가지고있고, $\overrightarrow{p}_{u}$를 원한다.
따라서 위 수식을 먼저 P로 풀어낸다.
$RQ\sum^{-1} = P$
이제 행렬 P에서 원하는 정보를 가져오면 된다.
'아카이브 > 추천시스템(2019)' 카테고리의 다른 글
| 추천시스템 18 - 경사하강법 (0) | 2019.08.05 |
|---|---|
| 추천시스템 16 - 사용자-사용자 협업필터링 코드예제 (0) | 2019.07.07 |
| 추천시스템 15 - 단항의 아이템 추천 (0) | 2019.07.07 |
| 추천시스템 14 - 아이템-아이템 협업필터링 (0) | 2019.07.07 |
| 추천시스템 13 - 사용자-사용자 협업필터링 (0) | 2019.07.01 |