
Model Free Control
Model Free Control은 다음과 같은 문제들을 풀기 위함이다:
- 문제에서 MDP가 주어져 있지 않지만, 경험을 통해 간단하게 만들 수 있는 경우
- MDP가 주어져 있지만, 환경이 너무 크기 때문에 샘플링을 통해 행동하는 경우
On-Policy vs Off-Policy
On-Policy
- 행동하면서 학습하는 문제
- 정책 $\pi$를 통한 경험의 샘플링을 통해 정책 $\pi$ 학습시키는 것 , 즉 행동하는대로 학습하는 형태
- 또한 검증시에도 같은 정책을 사용한다.
Off-Policy
- 다른 (에이전트의) 행동 패턴을 통해 학습하는 문제
- 다른 에이전트의 정책 $\mu$를 통핸 경험의 샘플링을 통해 정책 $\pi$를 학습시키는 것, 즉 다른 누군가의 행동을 보고 학습하는 형태
몬테카를로 정책 향상 (Policy Improvement)
다이나믹 프로그래밍에서는 정책 반복을 통해 정책을 발전 시켰다.

위 그림에서 화살표가 위로 향할 때 현재의 정책을 평가하고, 갱신된 정책함수를 얻게 된다. 그리고 아래로 향할 때 갱신된 정책함수를 사용해 탐욕적(greedy)으로 행동한다. 그리고 최후에는 최적의 정책으로 수렴하게 된다. Model-Free Control을 사용해서 이 두개의 반복적인 프로세스 사이에 어떠한 행위가 들어올 수 있는지 알아볼 것이다.
몬테카를로에서 위의 정책향상을 적용해 보겠다. 같은 상황에서 다이나믹의 방법이 아니라 몬테카를로의 방식으로 정책을 발전시키려면 어떻게 해야할까?
다이나믹의 방법을 그대로 적용하려면 두가지 문제가 생긴다.
- 상태 가치 함수를 사용하면 탐욕적으로 행동할 수 없다. 이는 상태만 알고있고, 행동(Action)은 모르기 때문이다. 따라서 상태 가치 함수가 아닌, 행동 가치함수를 사용해야 한다.
- 탐욕적으로 행동하다 보면, 탐색(Exploration)적인 문제가 생기는데, 탐욕적으로 행동하기 때문에 환경을 충분히 경험하지 못하게 된다.
따라서 탐욕적으로 아래의 Q(s, a)함수를 사용해 정책 향상을 해야 한다.
$\pi'(s) = argmax_{a \in A} Q(s, a)$
위의 수식을 사용해 가장 많은 보상을 얻을 수 있는 Q를 선택하게 된다.

상태 가치 함수가 아닌, 행동 가치 함수 Q를 사용해 탐욕적으로 정책을 발전시키는 방법이다. 화살표가 위를 향할 때 몬테카를로는 여러번의 에피소드를 실행하게 되고, 에피소드들의 평균 리턴값에 따라 Q함수를 평가하게 된다. 이를 평가하면 새로운 Q함수를 얻게 되고, 그를 통해 탐욕적으로 행동하면 최종적으로 수렴을 할 수 있게 된다. 하지만 탐욕적으로 행동하면 여전히 위에서 살펴본 같은 문제가 생긴다.
탐욕적 행동 선택

눈 앞에 두개의 문이 있다고 상상해보자. 이 중에 하나를 고르는 문제이다. (이런류의 문제를 밴딧 문제, Bandit-Problem 이라고 한다.) 아래의 경험을 살펴보자:
왼쪽 문을 열었더니 보상 0을 얻었다.
V(왼쪽문) = 0
오른쪽 문을 열었더니 보상 1을 얻었다.
V(오른쪽문) = 1
오른쪽 문을 열었더니 보상 3을 얻었다. (V는 평균)
V(오른쪽문) = 3
오른쪽 문을 열었더니 보상 2를 얻었다.
V(오른쪽문) = 2
위의 결과들을 보고 계속 탐욕적으로 행동한다면, 더이상 왼쪽문은 열지 않게 될것이다. 하지만 현실적으로는 왼쪽문은 더 경험하기 전까지는 왼쪽문이 어떤 가치를 주는지 알지 못하게 된다. (Local Optima에 빠지게 되는 것이다.)
E-greedy 탐색 (Exploration)
E-greedy (Epsilon Greedy)는 위의 문제에 대한 가장 간단한 해결책이다. 이 방법은 일정 확률을 사용한다. 이 $\epsilon$의 확률에 의해 랜덤한 액션을 선택하고, $1 - \epsilon$의 확률에 의해 Greedy한 액션을 선택한다.
$\pi(s|s) = \begin{cases} \frac{\epsilon}{m} + 1 - \epsilon, & \mbox{if}\ a* = argmax_{a \in A} Q(s, a) \\ \frac{\epsilon}{m} & otherwise \end{cases} $
간단한 아이디어 같아 보이지만, 이 방법을 통해 탐욕적 방법과 탐색을 모두 선택할 수 있게 되는 것이다.
E-greedy 정책 향상 (Policy Improvement)
E-greedy가 유용한 이유는, 이를 통해 정책 향상이 가능하기 때문이다. 따라서 위에서 보았던 화살표 그림에서의 아래를 향하는 화살표에 E-greedy를 적용할 수 있다는 뜻이다.
어떠한 e-greedy 정책 $\pi$에 대해, e-greedy 정책인 $\pi'$은 $q_\pi$에 대해 $V_\pi'(s) \geq V_\pi(s)$을 만족하는 정책 향상이 된다.
이 개념을 다시 몬테카를로 정책향상에 적용해보면 다음과 같은 그림이 나올 수 있다.

에피소드를 위의 정책을 사용해 진행하고 평가한다. 그리고 향상 스텝에서는 e-greedy를 적용한다. 이 정책은 확률적인(stochastic) 정책이 된다.
하지만 이는 약간의 효율성을 포기하는 것이다. 최종적으로는 최적 정책에 도달 하겠지만, 일정 확률로 랜덤한 액션을 취하기 때문이다. 따라서 이를 조금 더 효율적으로 만들어 보겠다.

몬테카를로는 여러번의 에피소드를 진행해 여러번의 리턴값들의 평균으로 정책을 갱신하게 된다. 이를 조금 바꿔 한번의 에피소드 진행마다 에피소드를 업데이트 하는 방식을 택하면 조금 더 빠르게 도달할 수 있게 되는 것이다. 그리고 평가는 조금 미루어 진행을 하는 방식이 된다.
GLIE
하지만 우리가 최적 정책을 찾으면서 충분한 탐색을 했다는 것을 어떻게 확인 할 수 있을까? 이를 위해서는 두가지의 밸런스를 잘 조정해야 한다. 이를 조정하기 위한 아이디어가 GLIE (Greedy in the Limit with Infinite Exploration)이다
GLIE는 다음 두가지 조건을 가진 일정한 탐색 시간을 정해놓는 방법이다.
- 모든 상태와 액션의 방문을 보장하기 위해서 모든 상태와 액션이 무한대로 탐색될 수 있도록 하는 것이다. 이를 통해 모든 상태와 모든 상태에서의 액션 조합이 최대한 많이 탐색될 수 있게 하는 것이다.
$\lim_{k \rightarrow \infty} N_k (s, a) = \infty$
- 정책은 결국 탐욕 정책으로 수렴할 것이다. 이는, 정책함수는 결국 최적의 보상을 얻는 방향으로 정책을 수정해 갈 것이기 때문이다.
$\lim_{k \rightarrow \infty} \pi_k(a|s) = 1(a = argmax_{a' \in A} Q_k(s, a'))$
GLIE 몬테카를로
샘플링된 K번째 에피소드에서 $\pi$: {$S_1, A_1, R_2, …, S_{\gamma}$} ~ $\pi$ 각각의 상태 $S_t$와 액션 $A_t$에 대해 다음과 같은 갱신 수식을 적용한다:
$N(S_t, A_t) = N(S_t, A_t) + 1$
$Q(S_t, A_t) = Q(S_t, A_t) + \frac{1}{N(S_t, A_t)} (G_t - Q(S_t, A_t))$
위 수식에서의 N은 카운터이다.
그리고, 정책은 시점에 따라 다음과 같이 갱신하고 발전한다. GLIE는 이 정책이 확률적인 정책에서 점진적으로 탐욕적인 정책이 되는것을 보장하게 된다.
$\epsilon = frac{1}{k}$
$\pi = e-greedy(Q)$
이를 통해 여러번의 배치 애피소드를 모아 갱신하는 방식보다 훨씬 효율적인 갱신을 할 수 있게 된다.
시간차 정책 향상
몬테카를로에 비교하면, 시간차 학습은, 에피소드를 끝까지 진행하지 않아도 학습할 수 있다는 이점이 있었다. 따라서 시간차 학습에 E-greedy알고리즘을 적용하면 Q함수를 매 시점마다 학습할 수 있게 된다.
SARSA
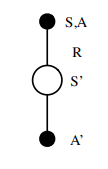
위의 방법을 통해 행동-가치 함수를 갱신하는 알고리즘을 SARSA라고 부른다. 위의 그림을 보면 왜 SARSA알고리즘인지 감이 올 것이다. SARSA는 하나의 상태 S에서 행동 A를 랜덤하게 샘플한 정책에 의해 선택하고 보상 R을 받는다. 그리고 새로운 상태 S'에 놓이게 되고 새로운 정책을 사용해 행동 A'을 선택하게 된다.
$Q(S, A) = Q(S, A) + \alpha (R + \gamma Q(S',A') - Q(S,A))$
위의 수식이 SARSA의 갱신 수식이다. 위 수식에 의하면, 기존의 Q값에 학습률 $\alpha$를 곱해진 새로운 가치를 조금 더해 갱신하게 되는데, 이 가치는 받은 보상과 감가율이 적용된 다음의 Q값을 더하고 현재의 Q값을 뺀 값이 된다. 수식에 의하면, 현재 상태 및 액션과 다음의 상태 및 액션만을 고려하 게 되는 것이다. (두개의 액션 모두 같은 정책을 통해 결정한다.)
SARSA를 사용한 Q함수의 갱신은 다음 그림에 표현되어 있다.

SARSA는 하나의 액션을 취할때 마다 Q함수를 갱신하게 되어있고 (모든 시점에 Q함수를 갱신한다는 의미이다.), Q함수는 E-greedy를 사용해 정책을 향상시키게 된다. 그리고 E-greedy에 의해 랜덤한 Exploration또한 수행하게 된다.
SARSA의 수렴
SARSA 역시 최적의 Q함수 즉 행동-가치 함수 Q(s,a) $\rightarrow$ $q_*(s,a)$로 수렴하게 되는데, 이는 GLIE의 정책 $\pi_t(a|s)$를 통해 수렴하게 된다. 또한 적절한 스텝 사이즈를 맞춰주어야 한다
N-스텝 SARSA 리턴
n = 1, 2, $\inf$ 에 대해서,
n = 1, (SARSA), $q_t^{(1)} = R_{t+1} + \gamma Q(S_{t+1})$
n = 1, $q_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2Q(S_{t+1})$
…
n = $\inf$ (MC), $q_t^{(\infty)} = R_{t+1} + \gamma R_{t+2} + … + \gamma^{T-1}R_T$
이전에 시간차 TD(0)에서 본 수식일 것이다.
SARSA역시 n-step이 무한대일때는 몬테카를로와 같아진다.
$q_t^{(2)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1}R_{t+n} + \gamma^nQ(S_{t+n})$
그리고 행동-가치함수 Q를 업데이트 하는 수식은 다음과 같다.
$Q(S_t, A_t) = Q(S_t, A_t) + \alpha((q_t^{(n)} - Q(S_t, A_t))$
SARSA($\lambda$)
SARSA 역시 $\lambda$ 리턴을 적용할 수 있다.
$(1 - \lambda)\lambda^{n - 1}$가중치를 사용해 N스텝의 Q값을 함께 고려하게 된다.
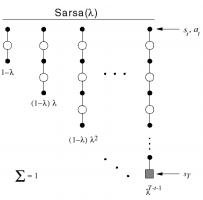
아래의 수식이 SARSA의 Forward View가 됩니다.
$Q(S_t, A_t) = Q(S_t, A_t) + \alpha(q_t^{(\lambda)} - Q(S_t, A_t)$
Backward View
SARSA의 Backward View에서도 Eligibility Trace 테이블을 사용한다. (테이블은 방문한 각 상태에 대해 저장해 놓는 테이블이다.) TD($\lambda$)와 다른점은 SARSA($\lambda$)는 각 상태 마다 상태-행동 페어에 대한 단 하나의 Eligibility Trace를 저장한다는 것이다.
$E_0(s, a) = 0$
$E_t(s, a) = \gamma\lambda E_{t - 1}(s, a) + 1(S_t = s, A_t = a)$
모든 상태s와 행동 a에서 Q(s, a)는 갱신이 되게 되는데, 이는 역시 TD-에러 $\delta_t$와 Eligibility Trace $E_t(s)$에 비례하여 진행 된다.
$\delta_t = R_t + 1 \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)$
$Q(s, a) = Q(s, a) + \alpha \delta_t E_t (s, a)$
Off-Policy Learning
지금까지는 On-Policy Learning에 대해서만 이야기했다. 이는 학습하는 정책이 평가하는 정책과 같은 방식이다. 하지만 많은 경우 학습하는 정책과 평가하는 정책이 달라야 하는 경우가 있다.
정책 $\mu$(a|s)를 따라 학습하고 있다고 가정해 보자.
하지만 평가에서는 타깃 정책인 $\pi$(a|s)를 사용해 $v_s$(s)나 $q_{\pi}$(s, a)를 구하게 된다.
이것이 중요한 이유는 여러가지가 있을 수 있다.
- 로봇이 사람이나 다른 에이전트를 통해 학습할 때
- 이전의 정책 $pi_1$, $pi_2$, … $pi_{t - 1}$을 통한 경험을 재사용하려고 할 때
- 실험적인 정책을 사용해 최적의 정책을 학습하려 할 때
- 하나의 정책을 사용해 여러개의 정책을 학습하려 할 때
결국 이를 정리하면, 다른 정책의 행동을 통해 현재 정책을 개선하려 할 때 사용하는 것이다.
중요도 샘플링
중요도 샘플링이란 현재의 분포 값을 추정하기 위해서 다른 분포에서 샘플링한 데이터를 사용해 추정하는 방법이다.
$E_{X~P}[f(X)] = \sum P(X)f(X)$
$= \sum Q(X) \frac{P(X)}{Q(X)}f(X)$
$= E_{X~Q}[\frac{P(X)}{Q(X)}f(X)]$
중요도 샘플링을 사용해 Off-Policy 몬테카를로나 Off-Policy 시간차학습을 구현할 수는 있다. 하지만 몬테카를로의 경우는 현실적으로 쓸모가 없을 정도로 성능이 좋지 않다.
Q러닝
Q러닝은 행동-가치함수 Q(s,a)를 Off-Policy 방식으로 학습하는 기법이다. 이 방식에는 중요도 샘플링이 필요하지 않다.
큐러닝은 다음 액션을 행동 정책 (학습하는 정책) $A_{t + 1} ~ \mu(-|S_t)$을 통해 결정하지만, 타깃 정책 (갱신&평가)할 때에는 $A' ~ \pi(-|S_t)$를 사용하게 된다.
이런 특성 때문에 중요도 샘플링이 필요하지 않게 되는데, 다음 수식에 표현되어 있듯이, 갱신 수식에서는 A'을 사용하게 되기 때문이다.
$Q(S_t, A_t) = Q(S_t, A_t) + \alpha (R_{t + 1} + \gamma Q(S_{t + 1}, A') - A(S_t, Q_t))$
Q러닝은 행동정책과 타깃정책을 모두 향상시키는 것이다.
타깃 정책 $\pi$는 greedy한 Q함수이다.
$\pi (S_{t + 1}) = argmax_{a'} Q(S_t+1, a')$
그리고 행동 정책은 e-greedy한 Q함수이다.
따라서 이를 정리하면,
$R_{t+1} + \gamma Q(S_{t+1}, A')$
$= R_{t+1} + \gamma Q(S_{t+1}, argmax_{a'} Q(S_{t+1}, a'))$
$= R_{t+1} + \max_a' \gamma Q(S_{t+1}, a')$
위 수식은 argmax를 한 뒤 다시 Q함수를 적용하기 때문에 최종적으로는 max의 Q함수를 찾게 되는 수식이다.

SARSA알고리즘은 그저 e-greedy 정책을 따라 탐험과 최적 정책을 모두 가져가려는 알고리즘이고, 탐험과 최적의 사이에서 갈등하는 문제가 있었지만, Q러닝은 정책과 탐험을 분리시키고, 행동은 e-greedy를 사용하고, 갱신은 최적의 greedy (max)를 사용해 갱신하는 방식으로 위의 문제를 해결한 것이다.
'아카이브 > 강화학습(2019)' 카테고리의 다른 글
| 강화학습 공부 - (3) Model Free Prediction (0) | 2019.08.13 |
|---|---|
| 강화학습 공부 - (2) 동적계획법 (0) | 2019.08.11 |
| 강화학습 공부 - (1) 마르코프 결정 프로세스 (0) | 2019.07.29 |