
동적 프로그래밍 (동적 계획법, Dynamic Programming)
"동적" (Dynamic) 이라는 단어는 순차적이고, 일시적인 방면의 문제를 푸는것이라는 것을 의미한다. 이는 복잡한 문제를 푸는 방법론이다.
- 큰 문제를 서브 문제들로 분해한다.
- 그리고 그 서브 문제들을 다 풀어내면, 큰 문제를 풀 수 있다.
동적 프로그래밍으로 풀 수 있는 문제들은 두가지 특성을 가지고있다.
- 최적의 세부구조를 가지고있다.
- 최적의 세부 구조들을 풀어내면, 그로 인해 원래의 문제가 풀리는 구조이다.
- 최적의 해를 찾기 위해 세부 문제들로 분해해야 한다.
- 겹치는 세부 문제들이 존재한다.
- 세부 문제들이 반복되어 일어난다.
- 또한 그 세부 문제들을 캐시(저장)하고 재사용한다.
- 따라서 그 세부 문제들을 반복해서 풀어내면 효율적으로 답을 구할 수 있다.
MDP는 위의 두가지 조건을 모두 만족한다.
- 벨만 방정식은 재귀적인 분해가 가능하다.
- 현재의 최적과, 남아있는 상태들의 최적을 구해야 한다.
- 가치함수를 저장하고 답을 구하기 위해 재사용할 수 있다.
동적 프로그래밍은 MDP에 관련된 모든 정보(모든 상태와 같은)에 대해 알고있다고 가정한다.
따라서 MDP를 계획하는데 사용된다.
예측을 위해서는:
- 입력: MDP <S, A, P, R, $\gamma>$, 정책 $\pi$ 또는 MRP <S, $P^*$, $R^*$, $\gamma$>
- 출력: 가치함수 $v_{\pi}$
조작(컨트롤)을 위해서는:
- 입력: MDP <S, A, P, R, $\gamma$>
- 출력: 최적 가치 함수 $v_*$와 최적의 정책 $\pi_*$
정책 평가 (Policy Evaluation)
문제: 주어진 정책 $\pi$를 평가하라
해답: 벨만 기대 방정식을 사용해 반복적(iteratively)으로 갱신한다.
- $v_1 \rightarrow v_2 \rightarrow … \rightarrow v_{\pi}$
- 임의의 상태 $v_1$에서 시작해 반복적으로 벨만 방정식을 사용해 가치를 구하면 끝가지 도달할 것이고, 그것이 곧 가치함수가 된다.
이를 위해 동기화 백업 방법을 이용한다.
- 각 반복 스텝에서는, 모든 상태 $s \in S$ 에 대해서 고려하고,
- s의 직후 상태인 s'에서 $v_k(s')$로부터 $v_{k+1}(s)$를 갱신한다.
$v_{k+1}(s) = \sum_{a \in A} \pi(a|s) (R^a_s + \gamma \sum_{s' \in S} P^1_{ss'} v_k(s')$
위의 수식은 현재 상태의 다음 상태에서의 가치함수를 정의하고 있기 때문에,
이를 반복적으로 수행하면, 동적 프로그래밍으로 MDP를 풀어낼 수 있다.
정책 반복 (Policy Iteration)
최적 경사를 찾기 위해서는 반복과 피드백을 통해 좋은 정책을 찾는 반복을 해야한다.
정책 $\pi$가 주어졌을 때, 우리는 더 좋은 정책을 찾고싶다.
먼저 정책을 평가한다.
이는 끝의 상태에 도달했을 때의 보상을 통해 평가된다.
$v_{\pi} = E[R_{t+1} + \gamma R_{t+2} + … | S_t = s]$
그리고 더 좋은 정책을 찾기 위해 greedy하게 $v_\pi$를 높이는 행위로 새로운 정책을 결정한다.
$\pi' = greedy(v_{\pi})$
이를 반복함으로서 우리는 최적 정책 $\pi^*$에 도달할 수 있게 한다.
예제: 렌탈
현실에서의 예제를 살펴본다.

MDP 정의:
상태: 두개의 렌탈 장소, 각각 최대 20개의 차가 있다.
(사람들은 각각의 장소에서 랜덤하게 렌트를 하거나 렌트가 끝난 차를 돌려줄 수 있다.)
액션: 최대 5개의 차를 밤 사이에 옮겨 놓는다. (다음날 수요를 생각해서 최적의 장소에 가져다 놓는다는 의미)
보상: 차를 렌트 하는데에 드는 비용 $10.
상태전환: 차들은 랜덤하게 렌트 요청 되거나 리턴될 수 있다.
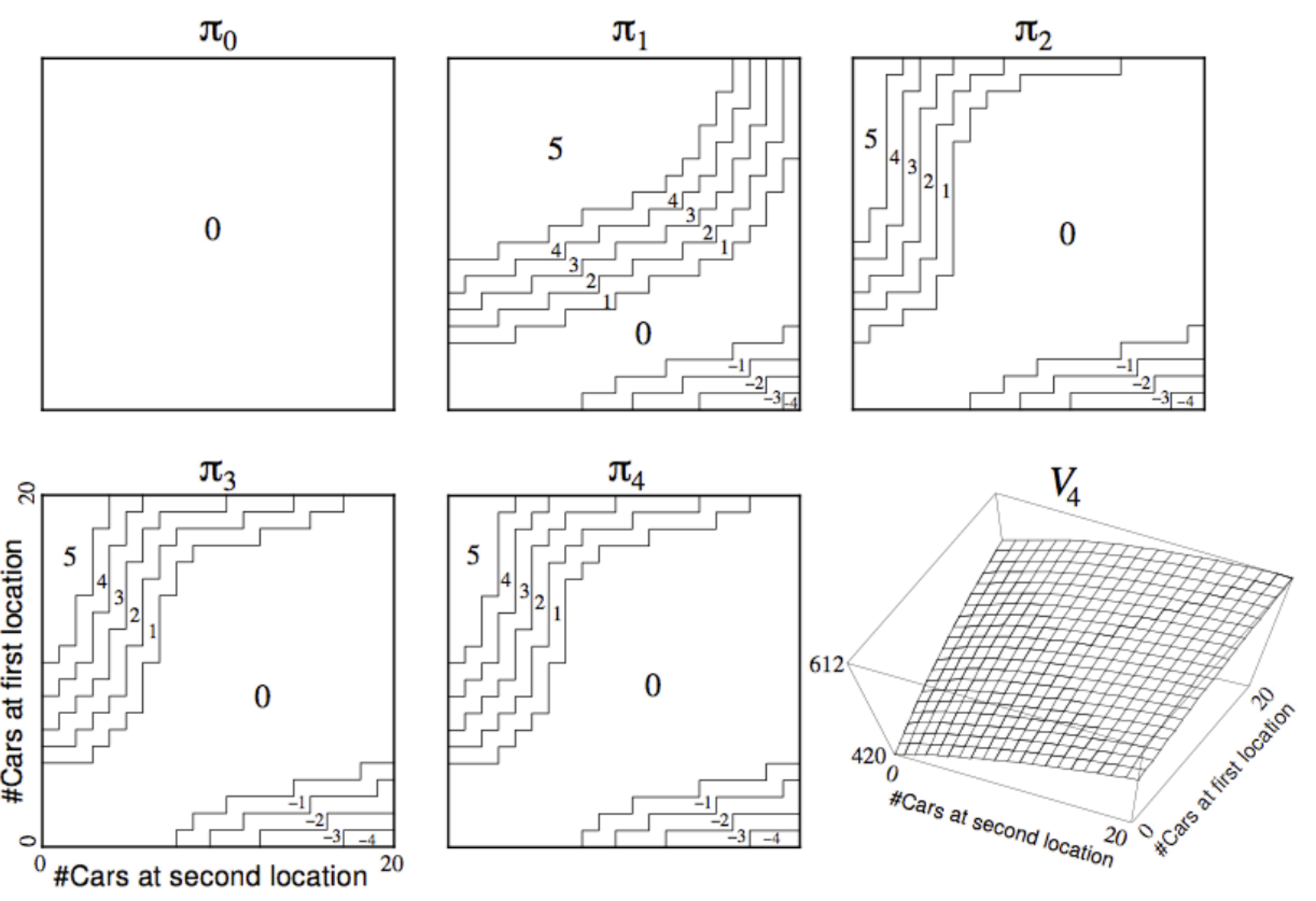
위의 그림을 보면 각 상태에서의 정책들을 표현하고 있다.
각각의 그래프는 확률을 표현하고 있고, 정책이 업데이트 될 때마다 그 확률을 조정하게 된다.
정책 향상 (Policy Improvement)

정책 반복과 정책 평가를 통해 최적 정책을 찾아가는 과정을 정책 향상이라고 한다.
이는 아래의 그림과 같이 항상 evaluation - improvement 사이클로 최적 정책을 찾을때 까지 이어진다.

결정론적 정책 (Deterministic) a가 있다, $ a = \pi(s)$
우리는 이 정책을 greedy하게 향상시킬 수 있다.
$\pi'(s) = argmax_{a \in A} q_pi(s, a)$
Greedy하게라는 의미는, 어떤 상태 a에서의 액션 a를 항상 바로 다음스텝에서 최대의 보상을 얻을 수 있게 결정한다는 의미이다. 그리고 q는 현재 얻을 보상 + 감가율이 적용된 다음의 보상들임을 기억하자.
$q_{\pi}(s, \pi'(s)) = \max_{a \in A} q_{\pi} (s, a) >= q_{\pi}(s, \pi(s)) = v_{\pi}(s)$
위의 수식의 의미는 다음 정책 \pi'가 현재의 정책에 따른 보상보다 많은 보상을 얻을 수 있다는것을 증명하는 것이다.
그리고 더 위의 수식 argmax를 넣음으로서, 최대의 보상을 얻어낼 수 있는 q함수를 통해 최대의 보상을 얻는 정책을 얻어낼 수 있다.
그리고 이 작업을 반복적으로 수행하게 되면 결국은 최적의 정책을 얻게 된다.
$q_{\pi}(s, \pi'(s)) = \max_{a \in A} q_{\pi} (s, a) = q_{\pi}(s, \pi(s)) = v_{\pi}(s)$
위의 수식은 결국 밸만방정식을 만족하는 것이고,
$v_{\pi} = \max_{a \in A} q_{\pi}(s, a)$
이는 곧 모든 상태에 대해 최적 정책을 찾았다는 의미이다.
$v_{pi}(s) = v_*(s) $ for all $s \in S$
Early Stopping
딥러닝에서 충분히 성능이 좋아졌다면, 일찍 학습을 끝내는 것 처럼, 정책이 충분히 좋아졌다면, 더이상 진행한다 해도 무의미할 때가 온다. 이런 방법을 Early Stopping이라고 한다.
두가지 방법이 있다 (딥러닝에서의 방법과 같다):
- Stopping Condition을 주어, 조건이 맞으면 멈추게 한다. 벨만방정식이 가치함수를 정해놓은 값보다 조금 업데이트를 하게 된다면 멈추는 방식이다.
- 반복 횟수를 정해놓는 것이다. 예를 들어, 100번의 반복을 했다면 충분하다고 보고 멈추는 방법이다.
최적 원칙 (Principle of Optimality)
모든 최적 정책은 두가지로 나눌 수 있다.
- 최적의 첫 액션 $A_*$
- 액션에 따른 상태 S'에서 얻어지는 최적의 정책
모든 상태에서 최적의 정책을 찾아낸 뒤, 처음 택할 액션이 무엇인가를 찾아내면, 해당 환경에서의 최적 정책을 찾아낼 수 있다.
법칙:
정책 $\pi(a|s)$가 상태 s에서 최적 가치함수 $v_{\pi}(s) = v_*(s) $를 얻어낼 수 있다면,
s에서 도달할 수 있는 모든 상태 s'들에 대해서,
정책 $\pi$가 s'에서도 최적 가치 $v_{\pi}(s') = v_*(s')$를 얻어낼 수 있을 것이다.
이는 곧 정답에서부터 최적 가치의 경로를 얻어내는, 즉 반대로 찾아내는 알고리즘이 되는 것이다.
가치 반복 (Value Iteration)
만약 우리가 s'에서의 최적 가치 $v_*(s')$의 정답을 알고있다면,
$v_*(s)$의 정답은 한스텝 전을 예측하는 것으로 찾을 수 있다:
$v_*(s) = \max_{a \in A} R^a_s + \gamma \sum_{s' \in S} P^a_{ss'} v_*(s')$
따라서 가치 반복은 위의 수식을 모든 상태에 대해 반복적으로 갱신하는 작업니다.
최후의 보상을 알고있고, 그를 통해 역추적하는 아이디어이다.
반복적인 MDP나 확률적 MDP에서도 잘 동작한다.
문제: 최적 정책 $\pi$를 찾는것
해답: 밸만 방정식의 응용을 통해 반복적으로 저장(backup)을 사용한 역추척
$v_1$ => $v_2$ => … => $v_*$
예제: 그리드월드

위와 같은 그리드월드에서 최적 경로를 찾는다고 할 때, 목표지점의 보상을 정하고, 목표지점에서 시작 해 모든 상태에서의 가치를 갱신할 수 있는 것이다.
'아카이브 > 강화학습(2019)' 카테고리의 다른 글
| 강화학습 공부 - (4) Model Free Control (0) | 2019.09.04 |
|---|---|
| 강화학습 공부 - (3) Model Free Prediction (0) | 2019.08.13 |
| 강화학습 공부 - (1) 마르코프 결정 프로세스 (0) | 2019.07.29 |