
강화학습
정책 평가 (Policy Evaluation)
정책 평가란 어떠한 정책에 대해 가치함수를 찾는 것이다.
이를 더 자세히 수식화 하면, 정책 $\pi$에 대한 상태-가치 $v_{\pi}$를 찾는 것이다.
$\pi \rightarrow v_{\pi}$
상태가치 벨만 방정식의 정의를 다시 살펴보자.
$v_{\pi}(s) \dot{=} \mathbb{E}_{\pi}[G_t | S_t = s]$
$v_{\pi}(s) = \sum_{a}\pi(a|s) \sum_{s'} \sum_{r}p(s',r|s,a)\left[r+\gamma \mathbb{E}_{\pi}[G_{t+1}|S_{t+1}=s']\right]$
이전에 봤던 다음과 같은 그리드 월드에서의 MDP는 선형대수(선형시스템)으로 푸는 것이 가능했다.
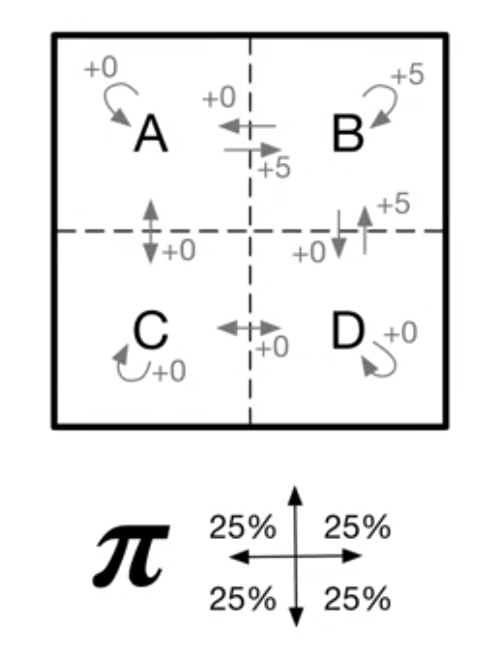
이러한 선형 시스템은 또한 다이나믹프로그래밍(동적계확법) 이라는 방식으로 더 효율적으로 풀수있다.

제어 (Control)
제어란 더 많은 보상을 얻기 위해 정책을 찾는 것이다.
다른 말로 하면 가치함수를 최대화 할 수 있도록 정책을 향상시키는 것이다.
이 제어가 바로 강화학습의 최종적인 목표이다.
하지만 이 제어를 하기 위해서 선행되어야 하는 것은, 정책이 어떠한 가치를 주는가를 먼저 평가하는 것이다.
정책 $\pi_1$이 정책 $\pi_2$보다 낫다는 것은,
모든 상태에 대해서

정책 $\pi_1$이 정책 $\pi_2$보다 같거나 더 큰 가치를 주어야 한다는 것을 기억하자.
제어란 더 나은 정책이 될 수 있도록 정책을 향상 시키는 것이고,
더이상 정책이 발전될 수 없을 때 이 정책을 $\pi_*$, 즉 최적 정책이라고 부른다.
따라서 제어의 목적은 다른말로 최적 정책 $\pi_*$를 찾는 것이 된다.
반복적 정책 평가 (Iterative Policy Evaluation)
다이나믹 프로그래밍(동적계획법)을 활용하면 정책평가를 반복적으로 효율적으로 할 수 있게 된다.
이 반복적인 절차는, 랜덤한 초기값에서 정책이 조금씩 나아지도록 갱신하는 방법이다.
이를 수식적으로 보면 이는 매우 간단하다.
$v_{k+1}(s) = \sum_{a}\pi(a|s) \sum_{s'} \sum_{r}p(s',r|s,a)\left[r+\gamma v_k(s')\right]$
$k$를 반복의 횟수라고 하면, $k+1$은 정책 평가를 한 뒤의 다음 단계가 된다.
이를 $k+1$이 $*$가 될 때까지 반복하면 되는것이다.
다른말로 하면 정책 평가를 진행했는데도 가치가 더이상 나아지지 않는다면,
우리의 가치함수가 $v_*$에 도달했다고 할 수 있는 것이다.
동적계획법은 메모리를 사용해 재귀적인 계산을 더 효율적으로 하는 방법이다.
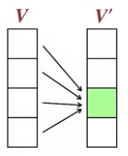
먼저 $V$를 현재 상태, $V'$을 다음 상태라고 한다면,
반복적으로 $V$의 상태에 대해서 정책 평가를 한 결과를 $V'$에 저장하고,
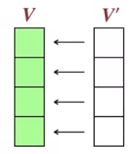
모든 평가가 끝나면 $V'$이 현재 상태가 되므로, $V$에 모든상태값을 복사한다.
물론 아래와 같이 바로바로 한 상태 평가시에 바로 갱신을 수행할 수도 있다.
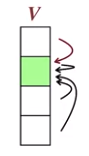
이러한 방법은 각 상태 갱신 시에 이미 갱신된 결과를 사용할 수 있어 더 빠른 수렴이 가능하게 된다.
다음은 정책 평가 반복의 알고리즘(Pseudo-code)이다.

'데이터사이언스 > 강화학습' 카테고리의 다른 글
| 강화학습 - (13) 가치 반복 (0) | 2020.10.03 |
|---|---|
| 강화학습 - (12) 정책 반복 (0) | 2020.09.28 |
| 강화학습 - (10) 벨만 최적 방정식 (0) | 2020.09.17 |
| 강화학습 - (9) 벨만방정식 (0) | 2020.09.14 |
| 강화학습 - (8) 정책과 가치 (0) | 2020.09.14 |