
선형성 (Linearity)
f(x)는 x라는 변수에 대한 함수이다.
f는 또한 연산(operation)이다.
f가 선형성을 가지려면 두가지 조건을 만족해야 한다.
1. Superposition (중첩)
$f(x_1 + x_2) = f(x_1) + f(x_2)$
만약 $x_1$과 $x_2$를 함수에 적용하기 전에 더한 것과,
함수에 각각 적용한 뒤 더한 것의 결과가 같으면,
중첩의 조건을 만족하는 것이다.
2. Homogeneity (동질성)
$f(a x) = a f(x)$
만약 x에 상수 a를 곱한 값에 함수를 적용한 것이,
함수에 적용한 뒤 상수 a를 곱해준 결과와 같으면,
동질성의 조건을 만족하는 것이다.
위를 하나의 수식으로 표현하면 다음과 같이 표현할 수 있다.
$f(a_1 x_1 + a_2 x_2) = a_1 f(x_1) + a_2 f(x_2)$
이러한 조건을 만족하는 연산을 선형성이 있다고 판단한다.
함수의 선형성
다음과 같은 수식이 있다면,
f(x) = mx
선형성은 다음을 만족하는 것이다.
$m(a_1 x_1 + a_2 x_2) = a_1 m x_1 + a_2 m x_2 $
$ = a_1 f(x_1) + a_2 f(x_2)$
이와 같은 수식은 다음과 같이 원점을 지나는 직선을 그리게 된다.

이렇게 원점을 지나는 것이 선형성을 판별하는 중요한 지표가 된다.
이를 증명하기 위해 다음 수식을 고려해보자.
f(x) = mx + n, $n \neq 0$
위 수식은 다음과 같이 원점을 지나지 않는 직선을 그리게 된다.
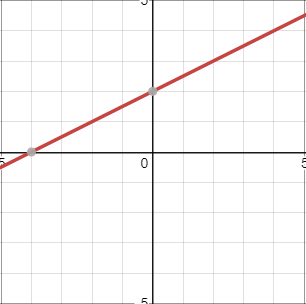
이를 다시 선형성을 만족하기 위한 수식에 대입해 보면,
$m(a_1 x_1 + a_2 x_2) + n \neq a_1 m x_1 + a_2 m x_2 $
위와 같은 결론이 나오게 된다.
따라서 이는 선형성을 만족하지 않게 된다.
연산의 선형성
이번에는 연산의 선형성을 판별해 보겠다.
하나의 연산을 다음과 같이 t에 대한 연산으로 정의 한다.
$x_1(t), x_2(t)$
다음 두가지의 연산을 고려해보자:
- 미분
- 적분
미분은 다음과 같은 등호를 만족한다.
$\frac{d}{dt}(a_1 x_1 (t) + a_2 x_2 (t)) = a_1 \frac{d}{dt} x_1(t) + a_2 \frac{d}{dt} x_2(t)$
적분 역시 다음과 같은 등호를 만족한다.
$\int (a_1 x_1 (t) + a_2 x_2 (t)) =a_1 \int x_1(t) + a_2 \int x_2(t)$
위와 같은 연산들은 모두 선형성을 갖고,
이들은 추후에 이야기할 행렬로서 연산이 가능하다.
행렬
행렬이란?

위와 같이 m개의 행과 n개의 열로 이루어진 수의 모임이다.
대각 행렬 (Identity Matrix)
$\mathbb{I}$라고 표기하는 행렬이다.
이는 다음과 같이 대각선은 1 이고, 나머지는 0인 행렬을 가리킨다.
$$\begin{bmatrix} 1 \quad 0 \quad 0 \\ 0 \quad 1 \quad 0 \\ 0 \quad 0 \quad 1 \end{bmatrix}$$
기본적으로 행렬은 교환법칙이 성립하지 않는다: $AB \neq BA$
하지만 대각행렬과의 교환법칙은 성립한다: $A\mathbb{I} = b\mathbb{I}$
역행렬 (Inverse Matrix)
역행렬이란, 행렬 A와 곱해졌을 때 $\mathbb{I}$가 되는 행렬을 말한다.
이러한 행렬은 다음과 같이 표기한다: $A^-1$
역행렬도 교환법칙이 성립할 때가 있다: $AA^-1 = A^-1A$
하지만 이는 항상 성립하는 것은 아니다. (가끔 예외가 있다.)
행렬 A의 역행렬은 다음과 같이 구할 수 있다.
$A = \begin{bmatrix} a \quad b \\ c \quad d \end{bmatrix}$
$A^{-1} = \frac{1}{ad - bc}\begin{bmatrix} d \quad -b \\ -c \quad a \end{bmatrix}$
행렬의 선형성
당연하지만 행렬 또한 선형성을 만족한다.
행렬 A가 있고, 벡터 $X_1$, $X_2$가 있다.
행렬의 연산은 보통 다음과 같이 표현한다.

행렬의 선형성을 증명해 보면 다음과 같다.
$A(a_1 x_1 + a_2 x_2) = a_1 A x_1 + a_2 A x_2$
위의 부등호는 성립하기 때문에 선형성을 만족한다.
행렬의 표기법
행 벡터 (row vector) $\mathbb{v} = (a, b, c)$
열 벡터 (column vector) $\mathbb{v} = \begin{bmatrix} a \\ b \\ c\end{bmatrix}$
- 행렬곱을 할 때에는 열 벡터로 표현하는 것이 유용하다
전치 (transpose) $\mathbb{v}^T$, $(a, b, c)^T$
선형결합
선형 결합이란 여러 벡터들을 특정 상수값의 합으로 표현하는 것이다.
다음 두개의 벡터가 있고,
$\mathbb{v} = \begin{bmatrix} a_1 \\ b_1 \\ c_1\end{bmatrix}$
$\mathbb{w} = \begin{bmatrix} a_2 \\ b_2 \\ c_2\end{bmatrix}$
이를 $\alpha$와 $\beta$라는 실수값으로 곱해주고 더한 것,
$\alpha \mathbb(v) + \beta \mathbb{w}$
$= \alpha \begin{bmatrix} a_1 \\ b_1 \\ c_1\end{bmatrix} + \beta \begin{bmatrix} a_2 \\ b_2 \\ c_2\end{bmatrix}$
이것이 $\mathbb(v)$와 $\mathbb(w)$의 선형 결합이 된다.
벡터는 이와 같이 열벡터로 표현하는 것이 더 좋은데,
이는 위와같은 선형 결합을 다음과 같은 행렬로 표현할 수 있게 되게 때문이다.
$\begin{bmatrix} a_1 \quad a_2 \\ b_1 \quad b_2 \\ c_1 \quad c_2 \end{bmatrix} $ $\begin{bmatrix} \alpha \\ \beta \end{bmatrix}$
$= \begin{bmatrix} \alpha a_1 + \beta a_2 \\ \alpha b_1 + \beta b_2 \\ \alpha c_1 + \beta c_2 \end{bmatrix}$
$= \alpha \begin{bmatrix} a_1 \\ b_1 \\ c_1 \end{bmatrix} + \beta \begin{bmatrix} a_1 \\ b_1 \\ c_1 \end{bmatrix}$
위와 같이 벡터들의 선형결합은 행렬과 변환이 될 수 있음을 기억해야 한다.
벡터
벡터란 원점으로 시작해서 각 차원에 해당하는 값을 가리키는,
물리적인 위치와 방향을 가지는 선을 말한다.
벡터 $\mathbb{v} = \begin{bmatrix} a \\ b \\ c\end{bmatrix}$가 있다면 v는 다음과 같이 3차원 평면에 표현될 수 있다.

벡터 덧셈
만약 다음 두개의 벡터를 더한다면, 각각의 원소를 더하면 된다.
$\mathbb{v_1} = (a_1, b_1, c_1)$
$\mathbb{v_2} = (a_2, b_2, c_2)$
$\mathbb{v_1} + \mathbb{v_2} = (a_1 + a_2, b_1 + b_2, c_1 + c_2)$
이를 기하학적 의미에서 보면, 다음과 같이 평행사변형을 그리고,
가운데를 가로지르는 벡터가 된다.
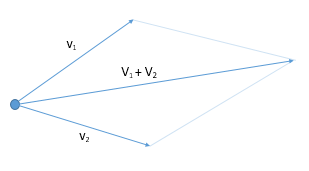
벡터 뺄셈
그렇다면 벡터의 뺄셈은 다음과 같이 표현될 수 있다.
(마이너스를 하는 벡터에서 시작해 당하는 벡터로 끝남)

벡터 내적 (Inner Product)
$v_1 \cdot v_2 = |v_1| |v_2| cos \theta$
벡터를 내적한다는 것은 곧 투영(projection)을 한다는 의미이다.
$v_1$과 $v_2$가 다음과 같이 있을 때, $v_1$과 $cos \theta$를 곱한 것은
기하학 적으로 다음과 같이 표현되고, v_2에서 투영한 직선까지의 거리가 그 값이 된다.
(벡터 사이의 각도가 $\theta$이다.)

따라서 내적의 의미는 반대편 벡터에 수직이 되는 선을 그어보고,
반대편 벡터($v_2$)에 현재 벡터($v_1$)의 성분이 얼마나 있는지를 알아보는 것이다.
또한 벡터 내적의 수식은 다음과 같이 성분을 모두 곱해 더한 값과 같다.
$v_1 \cdot v_2 = (a_1a_2 + b_1b_2 + c_1c_2)$
함수의 내적
함수의 내적은 다음과 같이 표현한다: $(f_1(t), f_2(t))$
f_1(t)를 선을 그리는 모든 y값이라고 표현하면,
각 함수들은 다음과 같이 무한대의 원소들을 갖게 되고,
$f_1(t) = (f_1(t_1), f_1(t_2) …)$
$f_2(t) = (f_2(t_1), f_2(t_2) …)$
이를 내적하면 모든 원소를 곱해 더하는 것이 되고, 다음과 같은 수식으로 표현할 수 있다.
$\sum^{\infty}_{k = -\infty} f_1(t_k) f_2(t_k)$
그리고 이는 적분으로 표현되고, 곧 두개의 함수를 곱해 적분한, 즉 넓이가 된다.
$\int f_1(t_) f_2(t_k) dt$
위에서와 같이 벡터의 원소가 되는 N차원의 유한한 값들을 다루는 것을 벡터공간이라고 하고,
이를 확장해서 함수에서 무한한 값을 벡터처럼 다루는 것을 힐버트 공간이라고 한다.
'데이터사이언스 > 선형대수' 카테고리의 다른 글
| 선형대수 - (6) 영공간 (Null Space) (0) | 2019.09.24 |
|---|---|
| 선형대수 - (5) 벡터공간 (0) | 2019.09.24 |
| 선형대수 - (4) 역행렬과 전치행렬 (2) | 2019.09.23 |
| 선형대수 - (3) LU 분할 (0) | 2019.09.23 |
| 선형대수 - (2) 가우스 소거법 (1) | 2019.09.04 |