
연립 방정식과 행렬
다음과 같은 연립 방정식이 있다고 하자:
(선형방정식은 1차식의 변수들만 존재하는 것이다.)
$\begin{cases} x + 2y = 3 \\ x + 5y = 6 \end{cases}$
위는 1번식에 4를 곱하고 2번식을 빼면, 3y = 6이 되고, y = 2라는 답이 나온다.
그리고 이를 대입해 x로 풀어내면, x = -1이라는 답을 얻을 수 있다.
위의 직선을 평면에 표현하면, x와 y는 두개의 직선의 교점임을 알 수 있다.
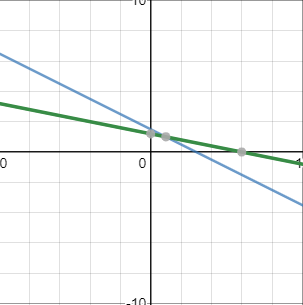
이를 컬럼벡터와 행렬을 통해 표현해 풀 수 있다.
위의 문제를 행렬과 벡터로 표현하면 다음과 같이 표현할 수 있다.
$\begin{bmatrix} 1 \quad 2 \\ 4 \quad 5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 3 \\ 6 \end{bmatrix}$
이는 두개의 컬럼 벡터의 선형 결합으로 표현될 수 있다.
$= x\begin{bmatrix} 1 \\ 4\end{bmatrix} + y\begin{bmatrix} 2 \\ 5\end{bmatrix}$
이는 각각의 벡터에 x와 y의 scala값을 곱해 더하면 (3, 6) 지점으로 해를 풀 수 있게 된다는 의미이다.
따라서 연립방정식은 다음 두가지 방법으로 표현될 수 있다:
- Row Form -> 교차점을 해로 찾게 된다.
- Column Form -> 열 벡터들의 선형 결합을 해로 찾게 된다.
Singular Case
연립방정식에서 해가 너무 많거나 해가 존재하지 않는 특이한(Unique 한) 경우를 Singular Case라고 한다.
- 해가 존재하지 않는 경우
- 해가 무수히 많이 존재하는 경우
해가 무수히 많은 경우 Row Form과 Column Form의 해석이 다르다.
- Row Form
- 직선이 평행(parallel)한 경우
- 직선이 겹치(overlap)는 경우
- Column Form
- 이는 위와 도형적으로 다른데, Row Form은 Row가 평행한 것이고, Column Form은 Column이 평행한 것이다.
- 세번째 벡터는 어떤식으로든 선형 결합을 하면 답에 적용될 수 있다.
- 두개의 벡터가 평행한 경우 (선형 결합을 구할 수 없다)
- 두개의 벡터의 선형 결합으로 이미 해를 구할 수 있는 경우
가우스 소거법 (Gaussian Elimination)
행렬을 사용해 선형 연립 방정식을 푸는 방법
다음과 같은 연립 방정식이 있다.
$\begin{cases} 2u + v + w = 5 \\ 4u -6 = -2 \\ -2u + 7v + 2w = 9 \end{cases}$
이 때 위의 연립 방정식을 푸는 방법은 다음과 같다.
1. 가장 위에 있는 방정식은 u의 계수가 0이 아닌 것으로 한다.
2. 첫번째 식에 적절한 수를 곱해서 두번째 식에 더하거나 빼준다.
[2] - [1] * 2
결과: -8u - 2w = -12
3. 세번째 식 역시 적절한 수를 곱해서 세번째 식에 더하거나 빼준다.
[3] - [1]
결과: 8v + 3w = 14
4. 두번째 식에 적절한 수를 곱해 세번째 식에서 더하거나 빼준다.
[3] + [2]
결과: w = 2
5. 결과가 나온 변수를 사용해 나머지 식에 대입해 다른 변수들을 구한다.
(식이 3개 이상이라면, 변수가 하나 남을 때 까지 위 2-4와 같이 수행한다.)
위의 풀이에서 더하거나 빼주는 변수 (2에서는 u, 3에서는 v, 4에서는 w)를 pivot이라고 한다.
가우스 소거법에서 pivot의 계수가 모두 0이 아닌 값이 될 때, 해를 갖는다.
도중에 0이 된다면 그것은 Singular Case가 된다.
이제 위의 연립 방정식을 행렬로 표현한다.
위의 식에서 변수를 제외하고 계수만 남겨 행렬을 만든다:
$\begin{bmatrix} 2 \quad 1 \quad 1 \\ 4 \quad -1 \quad 0 \\ -2 \quad 7 \quad 2 \end{bmatrix}\begin{bmatrix} 5 \\ -2 \\ 9\end{bmatrix}$
그리고 위의 순서를 따라 가우스 소거법을 수행한다.
$\begin{bmatrix} 2 \quad 1 \quad 1 \\ 0 \quad -8 \quad -2 \\ 0 \quad 8 \quad 3 \end{bmatrix} \begin{bmatrix} 5 \\ -12 \\ 14\end{bmatrix}$
$\begin{bmatrix} 2 \quad 1 \quad 1 \\ 0 \quad -8 \quad -2 \\ 0 \quad 0 \quad 1 \end{bmatrix} \begin{bmatrix} 5 \\ -12 \\ 2\end{bmatrix}$
마지막 행렬을 보면, 대각선 아래의 값들만 0이 된다.
이러한 행렬을 삼각행렬 또는 upper triangular 라고 표현한다.
삼각행렬을 만들어 낼 수 있다면, 각각의 변수에 대한 유니크한 해를 구할 수 있다.
Breakdown
Breakdown이란 Pivot이 0이 되는 경우
만약 가우스 소거법을 하는 도중에 pivot이 되어야 하는 값이 0이 된다면,
해가 있을 수도 있고 없을 수도 있게 된다.
이 때 해가 있는 상황에서는, 식들의 순서를 바꿔 풀어보면 된다.
이렇게 순서를 바꾸는 것을 pivoting이라고 한다.
다음은 이러한 상황의 예제이다.
$\begin{bmatrix} 1 \quad 1 \quad 1 \\ 2 \quad 2 \quad 5 \\ 4 \quad 6 \quad 8 \end{bmatrix} \begin{bmatrix} a \\ b \\ c\end{bmatrix}$
$\begin{bmatrix} 1 \quad 1 \quad 1 \\ 0 \quad 0 \quad 3 \\ 0 \quad 2 \quad 4 \end{bmatrix} \begin{bmatrix} a \\ b-2a \\ c-4a\end{bmatrix}$
이와 같은 상황이 발생한다면, 식의 순서를 바꿔 삼각행렬을 만들어 주면 된다.
$\begin{bmatrix} 1 \quad 1 \quad 1 \\ 0 \quad 2 \quad 4 \\ 0 \quad 0 \quad 3 \end{bmatrix} \begin{bmatrix} a \\ c-4a \\ b-2a\end{bmatrix}$
해를 구할 수 없는 경우
가우스 소거법을 수행하더라도 해를 구할 수 없는 경우가 있다.
다음 예제를 살펴보자.
$\begin{bmatrix} 1 \quad 1 \quad 1 \\ 2 \quad 2 \quad 5 \\ 4 \quad 4 \quad 8 \end{bmatrix} \begin{bmatrix} a \\ b \\ c\end{bmatrix}$
$\begin{bmatrix} 1 \quad 1 \quad 1 \\ 0 \quad 0 \quad 3 \\ 0 \quad 0 \quad 4 \end{bmatrix} \begin{bmatrix} a \\ b-2a \\ c-4a\end{bmatrix}$
이와 같이 두줄 모두 하나의 변수밖에 남지 않은 경우에는, 무수히 많은 해를 갖게 된다.
'데이터사이언스 > 선형대수' 카테고리의 다른 글
| 선형대수 - (6) 영공간 (Null Space) (0) | 2019.09.24 |
|---|---|
| 선형대수 - (5) 벡터공간 (0) | 2019.09.24 |
| 선형대수 - (4) 역행렬과 전치행렬 (2) | 2019.09.23 |
| 선형대수 - (3) LU 분할 (0) | 2019.09.23 |
| 선형대수 - (1) 선형성 (0) | 2019.09.02 |