머신러닝

본 포스팅은 Andrew Ng교수의 Machine Learning 코세라 강좌를 정리한 내용입니다.
https://www.coursera.org/learn/machine-learning
문제설정
J라는 함수가 있다고 하자, 우리는 이 함수를 minimize하는 알고리즘을 만들고자 한다.

먼저 θ0 과 θ1에 초기값 을 설정한다
그리고 θ0 과 θ1 가 minimum에 닿을 때 까지 J( θ0, θ1)를 감소시키고,
θ0 과 θ1값을 갱신한다.
경사하강법 과정 설명
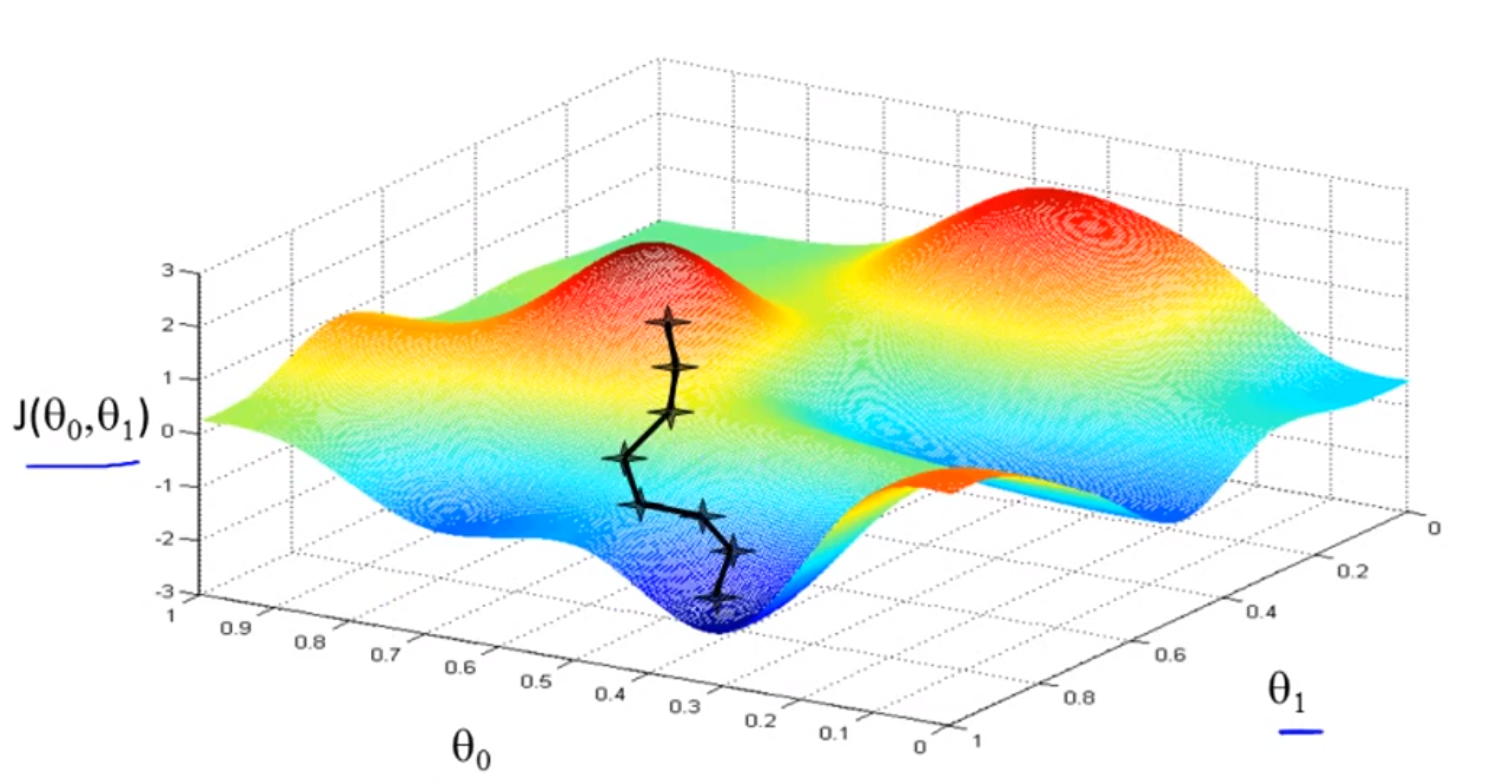
이 함수를 minimize하고자 한다고 하자.
먼저 θ0 과 θ1에 초기값 을 설정하고 시작한다.
가장 위의 그래프의 점이 θ0 과 θ1 의초기값이고, 내가 거기에 서있다고 가정해보자.
여러 방향을 살핀 뒤 한발을 밑으로 딛고 내려간다.
이러한 프로세스를 여러번 반복하다 보면, 이 그래프의 Local Minimum에 도달하게 된다.
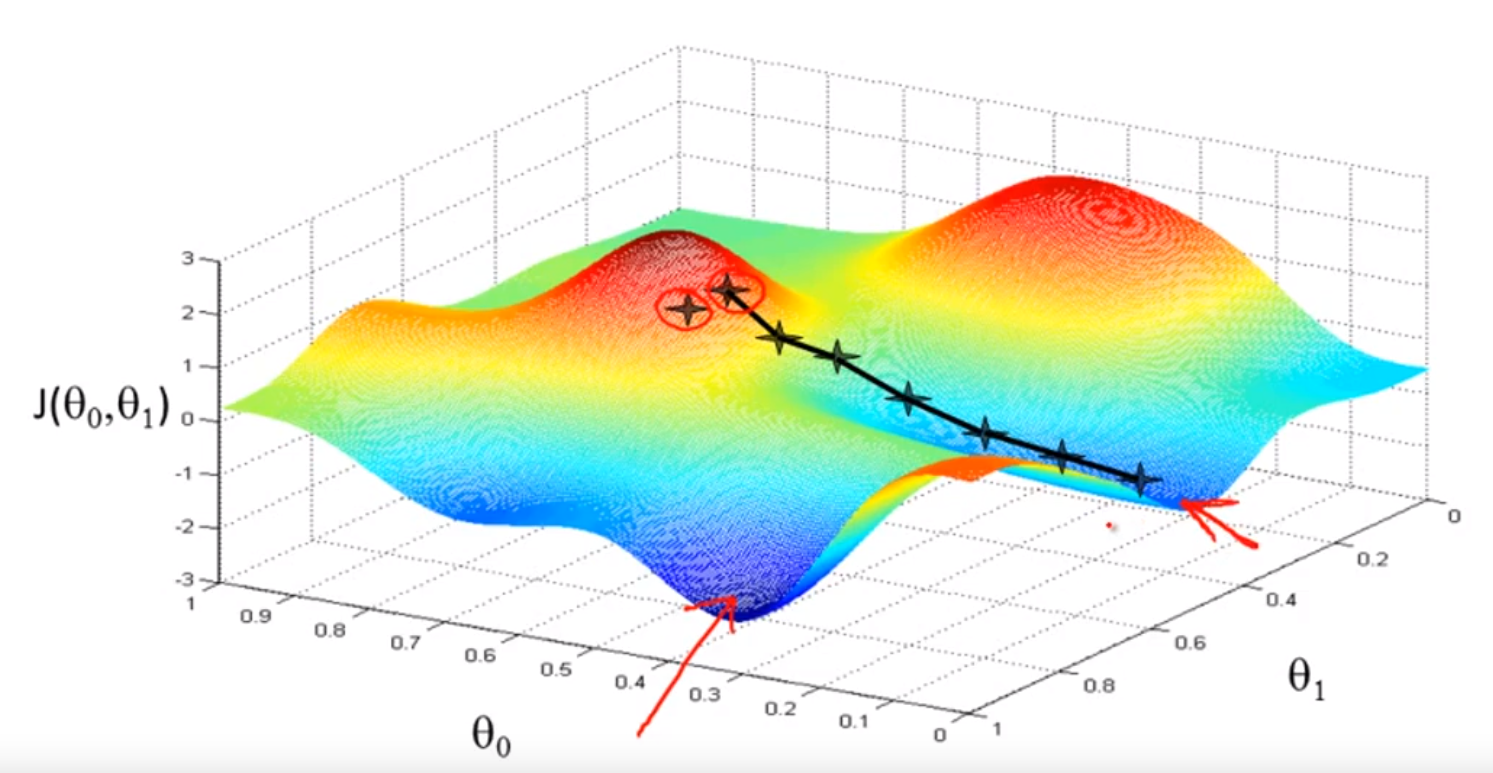
만약 다른 방향으로 첫 발을 내딛었다고 가정해보자.
그렇다면 경사하강법은 다른 Local Minimum으로 이끌게 될것이다.
경사하강법 알고리즘 정의
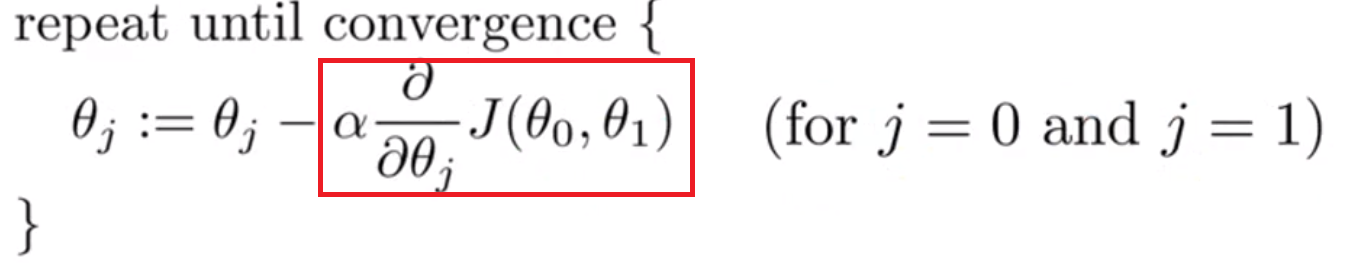
경사하강법은 먼저, 초기 θ값을 설정하고, 위 수식의 빨간색 박스 안에 있는 식으로 θ를 minimum에 닿을때까지 연속적으로 동시에 갱신하는 작업이다.
:= 표시는 Assignment를 의미한다.
- a := b 는 b를 a에 assign한다는 의미
α는 학습률을 의미하는데, 경사하강법에서 얼마나 큰 보폭을 내딛는지를 결정한다.
- α 값이 작으면 조금씩 내려가고, α값이 크면 빠르게 내려간다는 의미이다.
바로 뒤의 수식은 미분 수식인데, 나중에 설명하도록 한다.
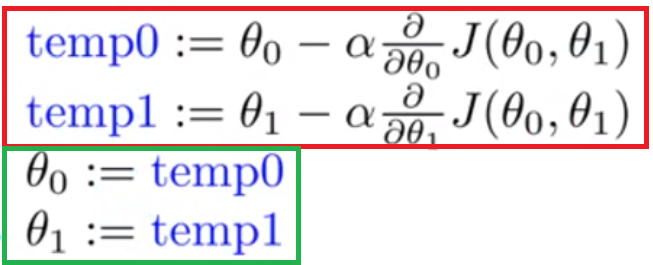
동시에 갱신한다는 것은 θ0 과 θ1에 대한 계산을 먼저 같이 하고, 그 후에 갱신을 같이 한다는 의미이다. 아래 수식을 보면 빨간색 박스를 먼저 계산하고, 그 계산이 끝난 후에 초록색 박스를 수행한다.

이렇게 하는 이유는, 아래 박스와 같이 θ0 을 먼저 갱신하면 그 계산이 temp1값에 영향을 주고 θ1이 의도했단 값과는 다른 값으로 갱신되기 때문이다.
경사하강법 예제 1)
J(θ1)가 2차 방정식이라고 가정하고 다음 도면에 경사하강법을 적용해보자.
(Θ1는 실수라고 가정한다.)

먼저 θ1에 임의의 초기 값을 부여하고 시작한다.
그리고 θ1을 다음 수식으로 업데이트 한다.
$\theta_{1} := \theta_{1} - \alpha * \frac{d}{d\theta_{1}} J(\theta_{1})$
(기본적으로 경사하강법에서는 여러개의 θ가 있고, 그 값들에 대하여 편미분을 사용하지만, 이 수식에서는 θ1가 하나밖에 없기 때문에, 편미분이 아닌 기본적인 미분으로 진행한다.)
위 수식을 현재 시점의 θ1에 대하여 미분하면, 기울기는 +값이 된다.
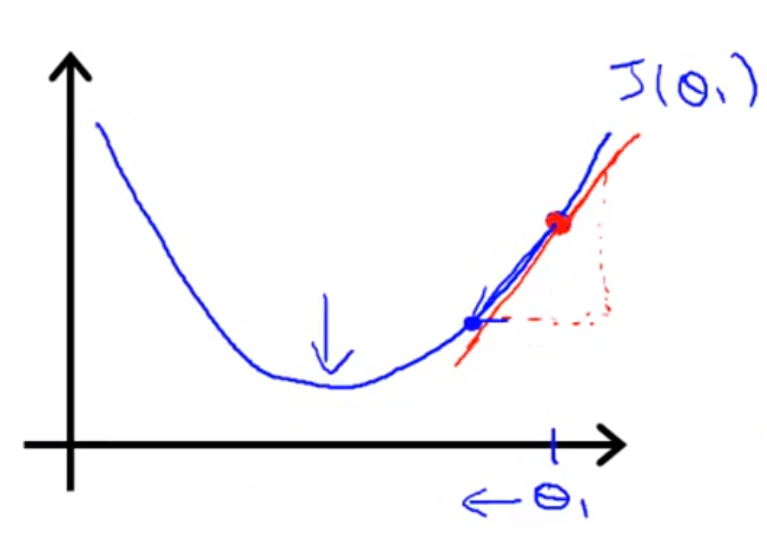
그리고 α값을 통해 θ1을 갱신하면 θ1은 작아지고 진행 방향은 왼쪽으로 가게 된다.
경사하강법 예제 2)
다른 예제를 살펴보자.
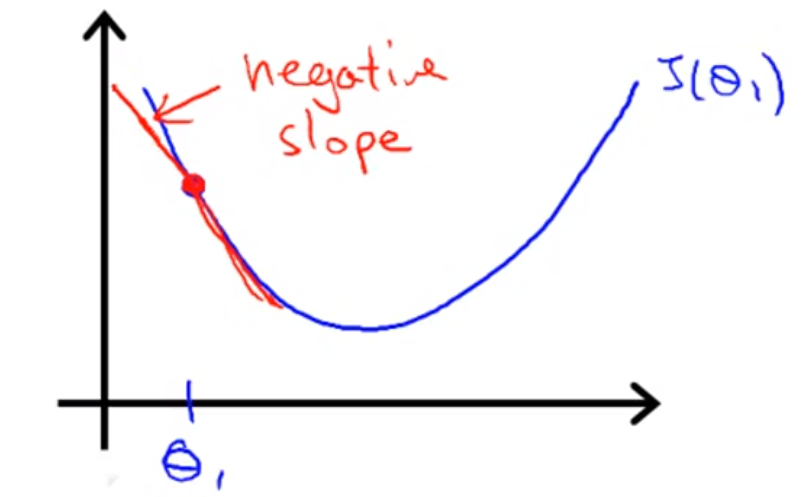
위의 지점에서 경사하강법을 진행한다.
해당 값에서 θ1에 대하여 미분하면, - 값의 기울기가 되고,
α값을 통해 θ1을 갱신하면 θ1값은 커지고 진행 방향은 오른쪽으로 가게 된다.
학습률
학습률은 위에서 설명했듯이, 경사하강법에서 경사의 폭을 결정한다.
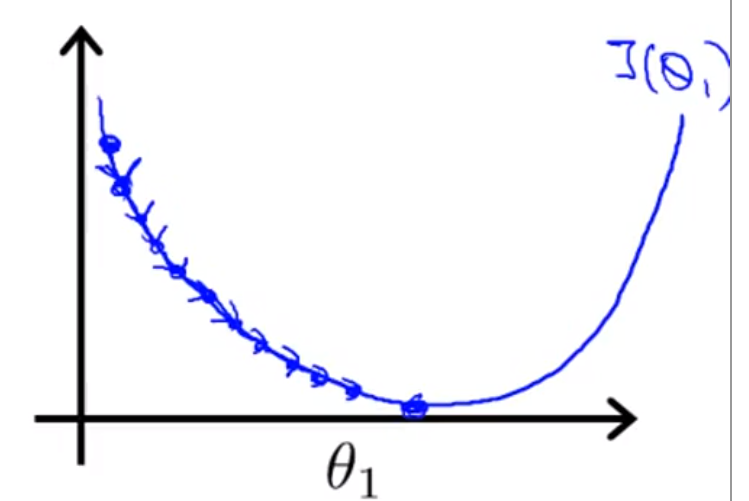
만약 학습률이 너무 작다면, 경사의 폭이 작아져서, 진행이 너무 느려지게 된다.
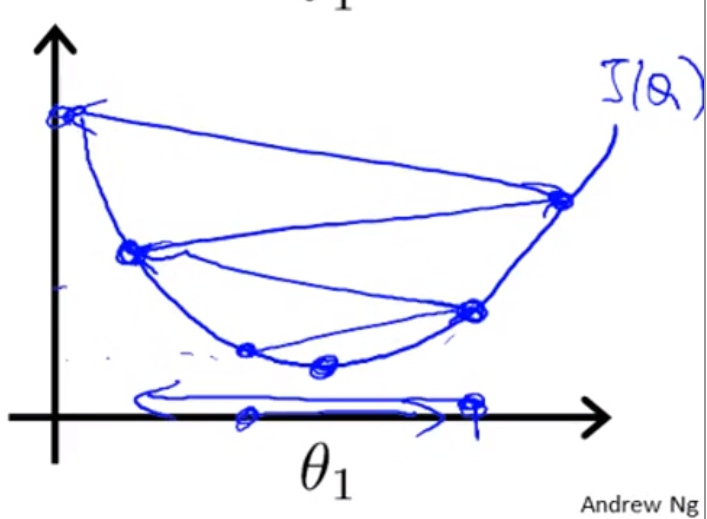
반대로 학습률이 너무 크다면, 경사의 폭이 커져서,
한번 갱신이 될 때, Local Minimum에 도달하지 못하고 이리저리 튀는 현상이 벌어지게 된다.
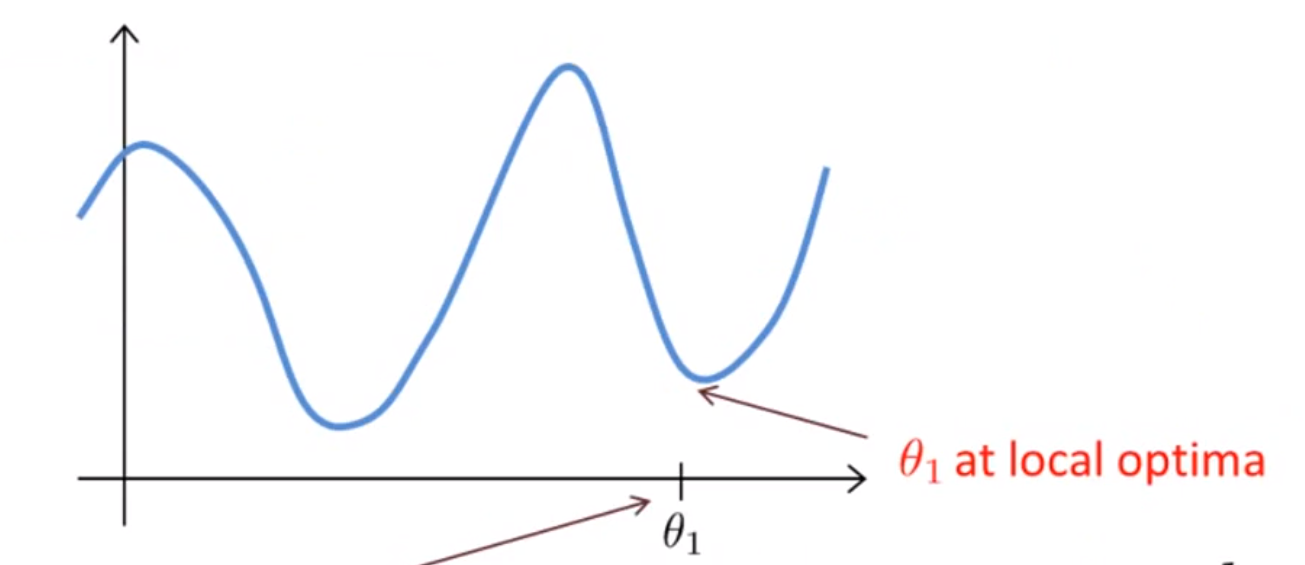
만약 θ1을 Local optima(Minimum)에서 시작하게 된다면,
미분값(아래의 수식에서의 빨간색 박스)이 0이 되기 때문에,
갱신이 일어나지 않게 된다.
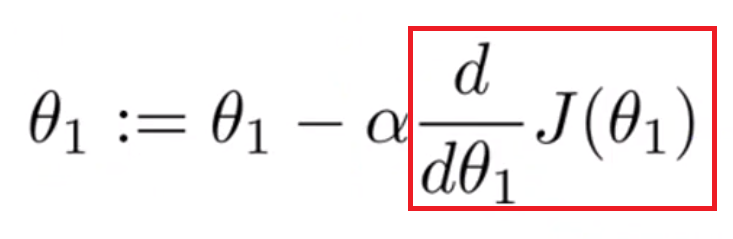
이 사실은 고정된 학습률 α값을 통해서 Local Minumum에 도달할 수 있다는 것을 증명한다.
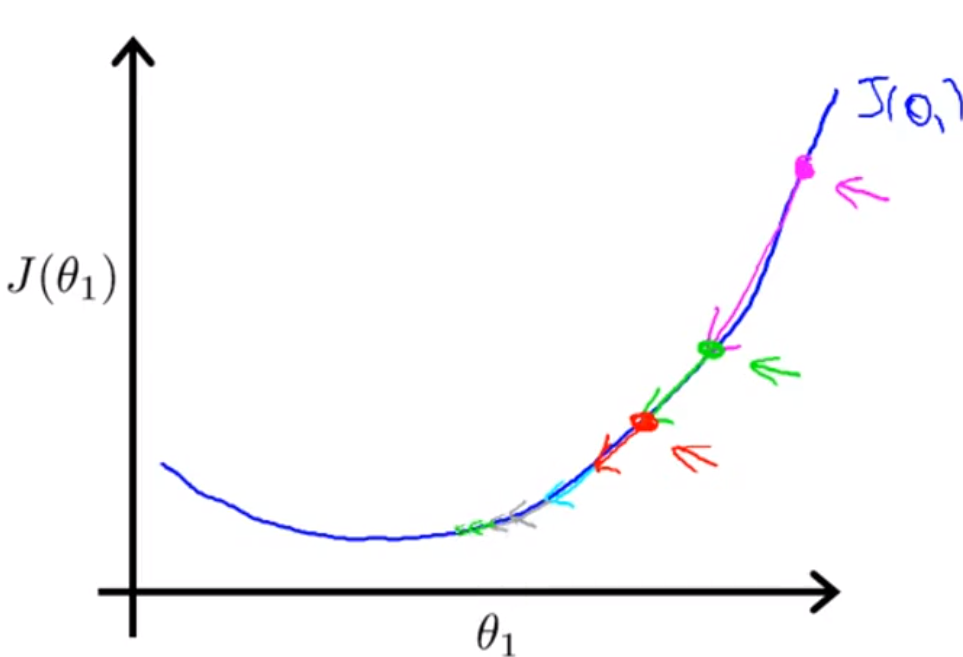
경사하강법은 매번 같은 값으로 갱신을 하는 것이 아니라, 그 시점의 미분값을 사용해 갱신하기 때문에,
기울기에 따라서 경사의 폭을 조정하게 된다.
따라서, 경사가 크면 폭을 크게 갱신하고, 경사가 작으면 폭을 작게 갱신하게 되기 때문에,
결국에는 Local Minimum에 도달하게 된다.
선형회귀에 적용
우선 선형회귀 수식을 다시 살펴보자.

선형회귀의 J수식에 경사하강법을 적용하려면, J를 미분해야 한다.
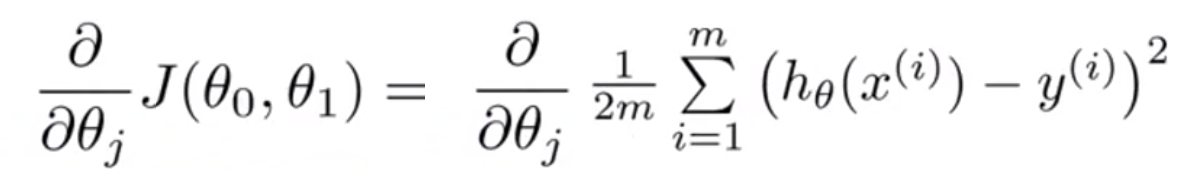
위 수식에 가설 함수를 대입하면 아래와 같은 수식이 된다.
$= \frac{\partial}{\partial \theta_{j}} \frac{1}{2m} \sum_{i=1}^{m} (\theta_{0} + \theta_{1}x^{(i)} - y^{(i)})^{2}$
그리고 j가 0일때와 j가 1일때의 값을 구한다.
각 θ값에 대해서 편미분을 진행하면 다음과 같은 수식이 된다.
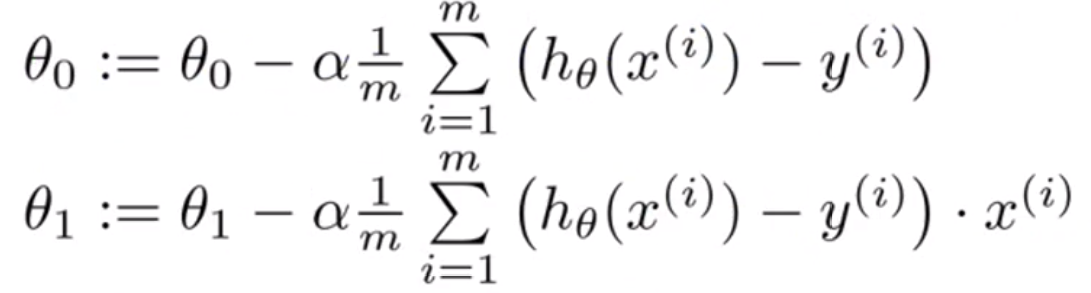
이 과정을 반복하면, 경사하강법을 수행하는 것이 된다.
선형회귀에서의 경사하강법 과정 설명
위의 경사하강법 설명과정을 보면 산맥(?)같은 3d그래프를 볼 수 있었다.
선형회귀의 비용함수를 그려보면 다음과 같은 모양이 나온다.
이 그릇과 같은 형태의 함수를 Convex Function이라고 부른다.

이 함수에서는 딱 하나의 Local Optima가 있게 된다.
이 Local Optima를 Global Optima라고 하는데, 선형회귀에서는 항상 이 Global Optima로 수렴하게 된다.
선형회귀에서의 경사하강법 예제)
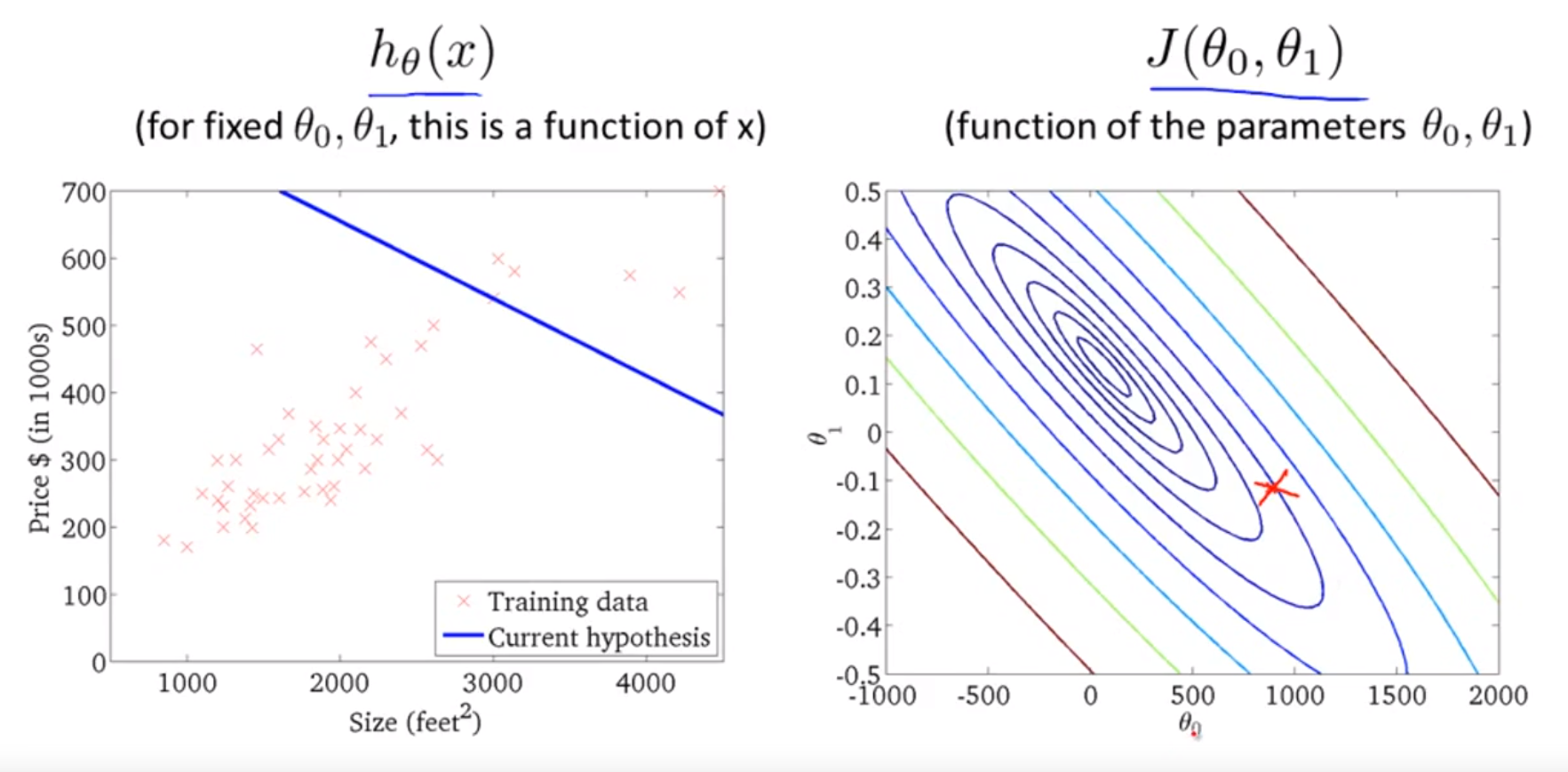
왼쪽에 가설 함수가 있고 오른쪽에 비용함수가 있다.
비용함수의 빨간지점에서 시작해 미분을 하면, 왼쪽의 가설함수 h를 바꾸게 되고, 그래프는 다음과 같이 바뀌게 된다.
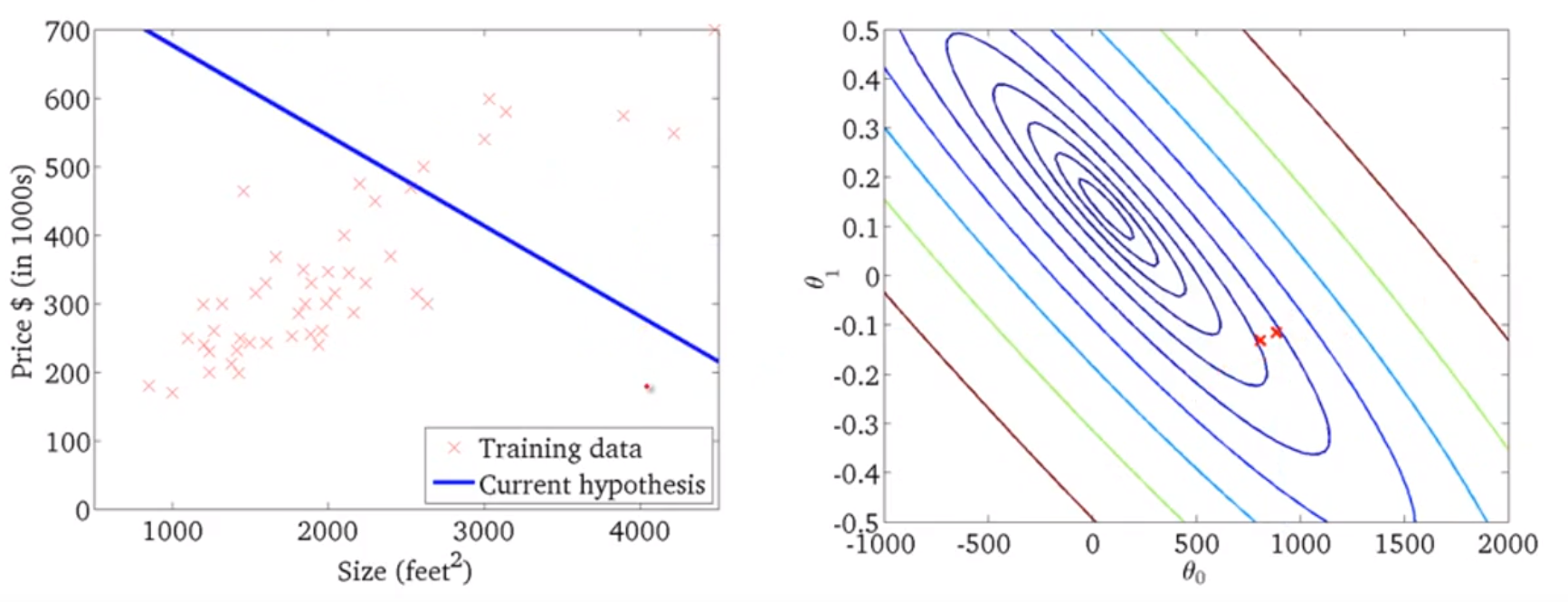
이 과정을 연속적으로 수행하게 되고 Global Minimum을 찾게 되면,
다음과 같이 데이터에 잘 맞는 선형회귀 함수를 만들어 내게 된다.
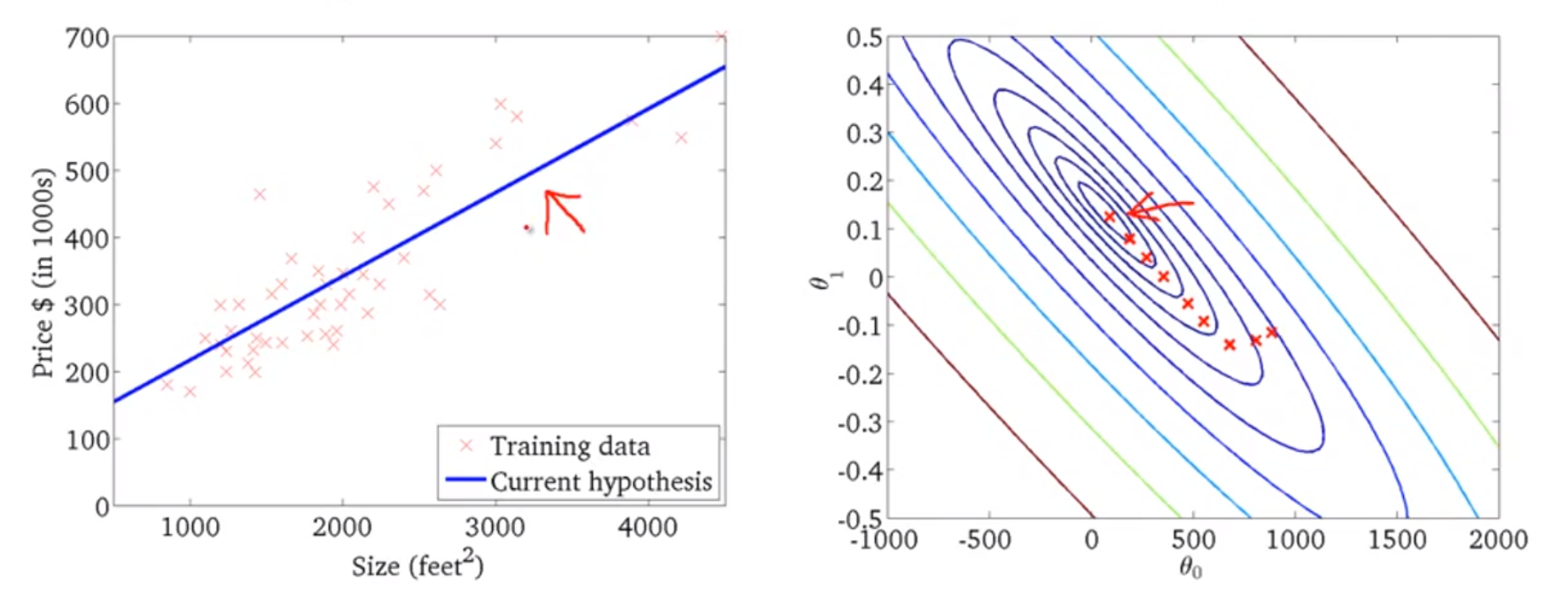
배치 경사하강법
배치란, 경사하강법의 한 스텝에서 학습데이터 전부를 사용하는것을 이야기한다.
'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 머신러닝 공부 6 - 경사하강법 트릭 (0) | 2019.06.29 |
|---|---|
| 머신러닝 공부 5 - 다중 선형 회귀 (0) | 2019.06.27 |
| 머신러닝 공부 3 - 비용함수 (0) | 2019.06.25 |
| 머신러닝 공부 2 - 단일변수 선형회귀 (0) | 2019.06.25 |
| 머신러닝 공부 1 - Intro, 지도학습, 비지도학습 (0) | 2019.06.23 |