머신러닝

본 포스팅은 Andrew Ng교수의 Machine Learning 코세라 강좌를 정리한 내용입니다.
https://www.coursera.org/learn/machine-learning
다중 선형 회귀
기존의 선형회귀에서는 하나의 입력 x값과 예측값 y값이 존재했다.
집값 예측 예제로 다시 돌아가보자. 현실 세계의 문제에서는 집의 크기만이 집값을 결정하지 않는다. 아래의 표를 보면, 집값은 크기 외에도, 방의 숫자, 층의 숫자, 연식 등의 정보들이 모두 가격에 영향을 줄 수 있다는 것을 보여준다.

앞선 포스팅에서 이야기 하였듯이, 이런 여러 변수들을 $x_{1}, x_{2}, x_{3}$와 같은 방식으로 표기하도록 하겠다.
몇가지 변수들을 더 정의해보면:
n은 특성의 갯수를 의미한다.
- 위의 예제에서 n의 4개이다.
$x^{(i)}$는 입력 특성중에 i번째 학습데이터를 의미한다.
- 위 예제에서$x^{(2)}$는 벡터 $\begin{bmatrix}1416, 3, 2, 40 \end{bmatrix}$ 이다.
$x_{j}^{(i)}$는 입력 특성중 i번째 학습 데이터의 실제 값을 의미한다.
- 위 예제에서$x_{3}^{(2)}$는 2이다.
가설함수
기존의 선형회귀에서의 가설함수는, θ값이 2개인 수식이었다.
위의 다변수의 집값예제에서는 수식이 다음과 같은 θ가 5개인 수식으로 바뀌게 된다.
$$h_{\theta}(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + \theta_{3}x_{3} + \theta_{4}x_{4}$$
편의를 위해 특성0번은 언제나 1로 정의한다. (θ0 값이 x없이 있는 이유이다.)
이를 보편적인 수식으로 다시 정의하면:
$$h_{\theta}(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + \theta_{3}x_{3} + ... + \theta_{n}x_{n}$$
위를 벡터형식으로 다시 표현하면 아래와 같이 되고,
$X = \begin{bmatrix}x_0, x_1, x_2, ..., x_n \end{bmatrix}$
$\theta = \begin{bmatrix}\theta_0, \theta_1, \theta_2, ..., \theta_n \end{bmatrix}$
행렬곱 $\theta^{T}X$를 수행하게 되면 위의 보편적인 수식과 같은 수식이 나오게 된다
(T는 행렬을 Transpose, 즉 전치 한다는 의미이다.)
경사하강법
가설함수의 변수 θ가 여러개라면, 비용함수의 θ도 여러개가 된다.
비용함수는 다음과 같이 바뀌게 된다:
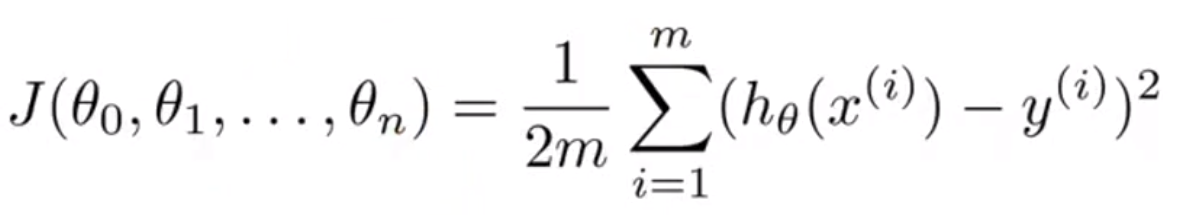
또한 이전 정의와 같이, 경사하강법은 위의 수식과 학습률을 사용해 θ들을 동시에 갱신하는 작업이 된다.

θ가 한개일 때는, 0과 1에 대한 값만 구하면 됐지만, 다변수일 경우에는 시그마를 사용해 모든 값을 더해준 것을 볼 수 있다.
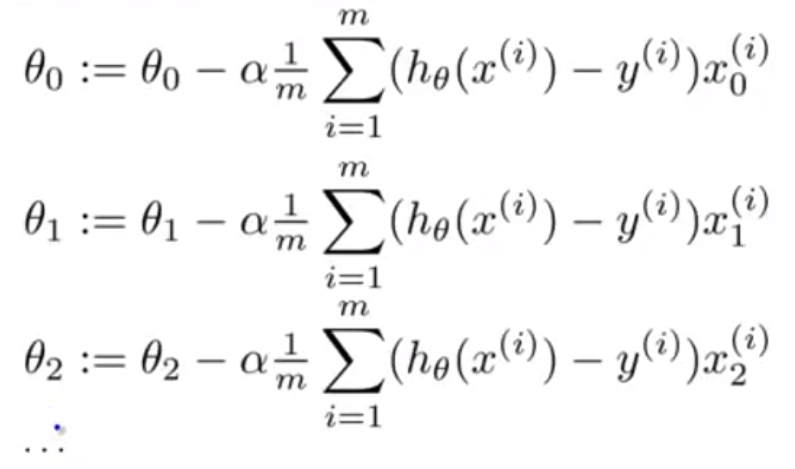
Θ의 수만큼 동시에 갱신하는 작업을 진행하게 된다.
(x0 = 1이고, 나머지 수식들에는 n번째 x가 곱해지게 된다.)
'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 머신러닝 공부 7 - 정규방정식 (0) | 2019.06.29 |
|---|---|
| 머신러닝 공부 6 - 경사하강법 트릭 (0) | 2019.06.29 |
| 머신러닝 공부 4 - 경사하강법 (0) | 2019.06.26 |
| 머신러닝 공부 3 - 비용함수 (0) | 2019.06.25 |
| 머신러닝 공부 2 - 단일변수 선형회귀 (0) | 2019.06.25 |