머신러닝 공부 7 - 정규방정식

머신러닝

본 포스팅은 Andrew Ng교수의 Machine Learning 코세라 강좌를 정리한 내용입니다.

https://www.coursera.org/learn/machine-learning

정규방정식

정규방정식 이란 특정 선형 문제에서 파라미터값인 θ를 더 쉽게 풀 수 있게 만들어주는 방법이다.

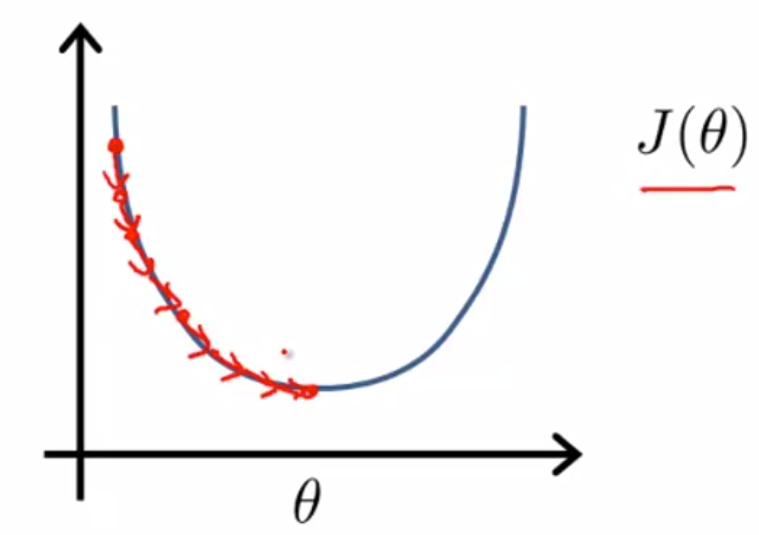
지금까지의 경사하강법에서는, Global Minimum을 찾기 위해 많은 스텝들을 밟아야 했다.

하지만 정규방정식은 이것을 분석적으로 풀 수 있게 해준다.

경사하강법의 많은 반복을 하기보다, 분석적으로 θ값의 해를 구하면 한번에 구할 수 있다는 말이다.

 

예제)

변수가 많지 않은 아래 2차 방정식 수식을 보자.

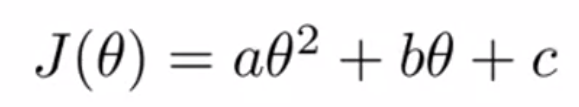
위의 수식을 minimize하려면 미분 값을 구한 다음, =0을 하고 θ로 풀면 된다.

 

하지만 많은 문제들은 변수 θ가 2개에서 끝나지 않는다.

이런 문제들은 어떻게 minimize를 할 수 있을까?

위의 수식을 풀 수 있는 방법은, 각 θ값에 대해 편미분을 하는것이다.

하지만 우리의 목적은 미분 없이 이것을 구하는 것이다.

 

집값 예제)

집값예제로 다시 돌아가보자. 우리는 m=4의 특성들을 가지고있다.

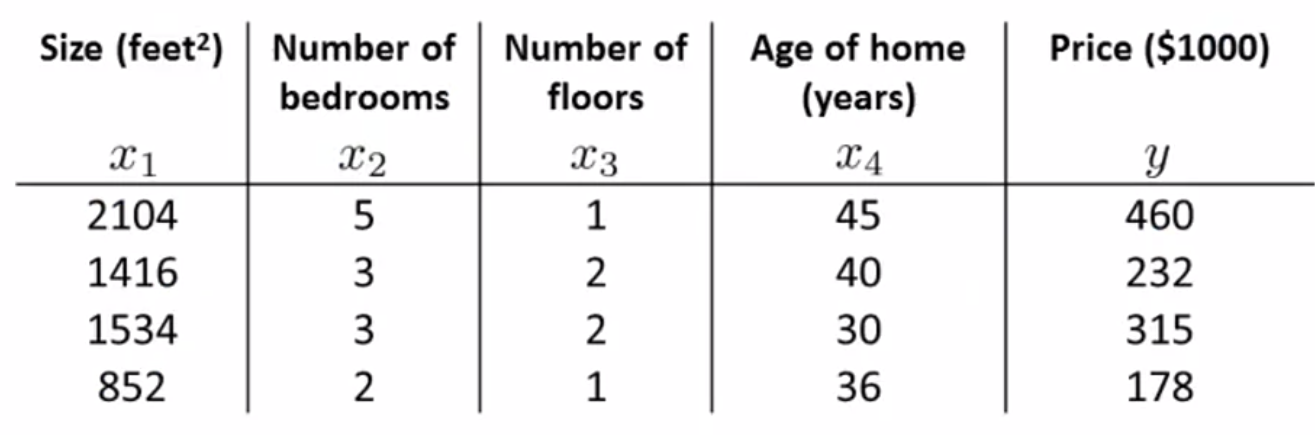
이 테이블에 아래와 같은 x_0 컬럼을 더 더한 후,

이 값들을 하나의 행렬로 만들어 보겠다.

같은 방법으로 y값도 하나의 벡터로 만든다.

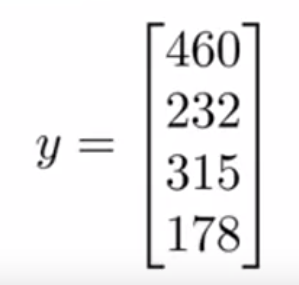
이 때 X는 m x (n+1)차원의 행렬이고, y는 m개의 값을 가진 벡터이다.

그리고 이 행렬과 벡터를 이용해 다음 수식을 구하면, 최소값을 가지는 θ들을 구할 수 있다.

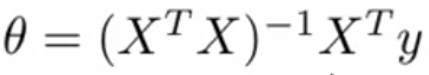
공식

위의 프로세스를 공식화해 보겠다.

m개의 학습 데이터가 있고$(x^{(1)}, y^{(i)}), ... ,(x^{(m)}, y^{(m)})$ , n개의 특성이 있다.

하나의 학습데이터의 x값 들은 n개의 원소를 가진 벡터들로 이루어져있고,

이 벡터들을 사용해 행렬 X를 구축한다. (이 행렬을 다른말로 디자인행렬이라고 부른다.)

$$X = [(x^{(1)})^{T}, (x^{(2)})^{T}, ... ,(x^{(m)})^{T}]$$

m개의 학습 데이터들의 y를 모으면 하나의 벡터를 만들 수 있고,

행렬 X와 벡터 y를 이용해, 다음 수식에 대입하면 된다.

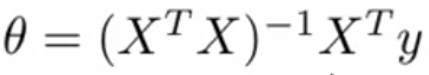
(역행렬과 행렬 전치에 대한 설명은 생략하겠다.)

 

경사하강법 vs 정규방정식

경사하강법	정규방정식
학습률 α값을 결정해야 한다. 많은 반복을 요구한다. 많은 양의 특성(n)에도 잘 동작한다.	학습률 α값을 정해줄 필요가 없다. 반복이 필요없다. 수식 (X^T X)^-1을 풀어야 한다 특성의 갯수(n)가 많아지면 너무 느려진다. (행렬전치, 행렬곱, 역행렬을 구하는데 O(n^3)의 계산시간이 걸린다.

 

역행렬을 구하지 못한다면?

역행렬을 구할 수 없는 행렬들이 종종 있다. 이러한 경우에는 다음과 같응 방법을 고려해 볼 수 있다.

• 특성의 양을 줄여 역행렬이 가능한 행렬을 만든다.
• 사용 가능한 정규화 방법을 사용한다.