머신러닝

본 포스팅은 Andrew Ng교수의 Machine Learning 코세라 강좌를 정리한 내용입니다.
https://www.coursera.org/learn/machine-learning
분류문제
X를 입력데이터, Y를 출력이라고 할 때, Y가 이산의 값인 문제를 분류문제라고 한다.
다음과 같은 예제들이 있다:
- 이메일이 스팸인지 아닌지 분류
- 온라인 거래가 사기인지 아닌지 분류
- 종양이 악성인지 양성인지 분류
이런 분류문제에서는 y값이 1이면 Positive, 0 이면 Negative로 분류하게 된다.
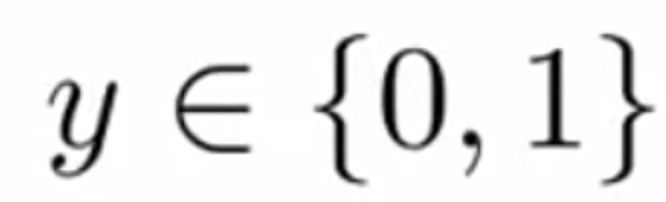
유방암예제)
악성종양예제를 살펴보자

위 데이터셋에 대한 출력값은 0/1로 나뉜다.
이런 데이터셋에서는, 회귀문제와 같이 데이터셋과 알맞는 직선을 그리면 안된다.
이런 문제를 푸는 방법은, 어떠한 임계값 즉 0.5를 임계값으로 두어,
$h_\theta(x) >= 0.5$ 이면 y = 1로
$h_\theta(x) < 0.5$ 이면 y = 0으로로
분류하게 하면 된다.
이러한 문제를 분류할 때는, 두 종류의 데이터를 나누는 직선을 그리게 된다.
위의 문제에서는 다음과 같은 직선을 그릴 수 있을것이다.
(사실 어떠한 직선이든 두 데이터셋을 나눌수만 있으면 된다.)

회귀와 분류
회귀모델이 분류문제와 맞지 않는 이유가 몇가지 있다.
- 선형회귀는 데이터에 맞는 직선을 그리게 되는데, 데이터를 분류하는 선을 그려야 한다.
- 회귀값은 주어진 데이터에 대한 실수값을 출력하게 되어있는데, 분류값은 0혹은 1값이어야 한다. (회귀값은 0보다 작거나 1보다 큰 값들이 나올 수 있다.)
이를 해결할 수 있는 회귀법이 있는데, 바로 로지스틱 회귀이다.
이 모델은 역사적인 이유때문에 회귀라고 불리지만, 분류모델이다.
가설함수
회귀를 이용해 분류문제를 풀기 위해서는 가설함수를 조금 바꿔야 햔다.
그 이유는 $h_\theta(x)$를 0에서 1사이 값 즉, $0 <= h_\theta(x) <= 1 $로 표현해야 하기 때문이다.
따라서 기존 $h_\theta(x)$를 다음과 같이 다시 표현해보도록 하겠다.
$$h_\theta(x) = g(\theta^{T}x)$$
함수 g는 다음과 같다:
$$g(x) = 1 / 1 + e^-z$$
이 함수의 이름은 시그모이드(Sigmoid)또는 로지스틱 함수라고 하는데,
로지스틱회귀의 이름은 이 로지스틱에서 따온것이다.
시그모이드 함수를 그래프로 그려보면 다음과 같이 나온다.
그래프를 보면 모든 값들은 0과 1사이의 값인것을 볼 수 있다.

x가 $\infty$로 가면 g(x)는 1이 되고 x가 $-\infty$로 가면 g(x)는 0이 된다.
출력값의 의미
$h_\theta(x)$의 출력값은 x가 주어졌을 때 y가 1일 확률이다.
예) 환자가 유방암이 있을 확률을 70%라고 하면, $h_\theta(x) = 0.7$인 것이다.
이를 조금 더 공식적으로 표기하면:
$$h_\theta(x) = P(y = 1 | x;\theta)$$
결국 위 수식의 h는 x에 $\theta$가 주어졌을 때 y가 1일 확률인 것이다.
이 결과를 사용해 우리는 y를 0또는 1의 값으로 만들어 내야 한다.
따라서 우리는 y가 0일 확률도 알아야하는데 이를 구하는 방법은 다음과 같다:
$$P(y = 0|x;\theta) = 1 - P(y = 1|x;\theta)$$
모든 확률을 더하면 1이고, y가 1일 확률과 0일 확률을 더한값 역시 1이 되어야 하기 때문에 y가 0일 확률은 곧, 1 - (y가 1일확률)이 되는것이다.
결정경계 (Decision Boundary)
앞서 언급했듯이 g(x)는 $h_\theta(x)$의 결과를 시그모이드 함수에 적용하는 것이다.
그 결과를 0과 1로 만드려면 다음과 같이 하면 된다:
$h_\theta(x)$의 값이 0 이상 즉, $g(x) >= 0.5$ 이면 "y = 1"
$h_\theta(x)$의 값이 0 미만 즉, $g(x) < 0.5$ 이면 "y = 0"
위는 다시말해 $\theta^{T}x$의 값에 시그모이드를 적용한 값이 0.5 이상이면 1, 0.5 미만이면 0으로 대체해주면 된다는 의미이다.
예제)
다음과 같은 가설함수가 있다:

$\theta$의 값이 [-3, 1, 1]일 때, $-3 + x_1 + x_2 >= 0$를 만족하면 "y = 1"인 상황이 된다.
이를 풀어보면, $x_1 + x_2 = 3$이 되는데,
이를 그래프에 그려보면 다음과 같다:

그래프를 자세히 보면, 직선의 위의 값들은 모두 x이고 아래의 값들은 모두 o이다.
따라서 데이터셋의 어떤 데이터든, $\theta_0 + \theta_1x_1 + theta_2x_2 >= 0$을 만족하면 1 그렇지 못하면 0이 되는 것이다.
그리고 위의 직선이 가설함수에 의해 데이터를 분류하기 때문에 이를 결정경계라고 부른다.
'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 머신러닝 공부 7 - 정규방정식 (0) | 2019.06.29 |
|---|---|
| 머신러닝 공부 6 - 경사하강법 트릭 (0) | 2019.06.29 |
| 머신러닝 공부 5 - 다중 선형 회귀 (0) | 2019.06.27 |
| 머신러닝 공부 4 - 경사하강법 (0) | 2019.06.26 |
| 머신러닝 공부 3 - 비용함수 (0) | 2019.06.25 |