머신러닝

본 포스팅은 Andrew Ng교수의 Machine Learning 코세라 강좌를 정리한 내용입니다.
https://www.coursera.org/learn/machine-learning
비용함수
다음과 같은 학습데이터가 있고, 가설함수가 있다.

이 때, θ는 파라미터, 즉 매개변수라고 한다.
이 매개변수들은 어떻게 결정될까?
가설함수 h0(x) = θ0 + θ1x 에 대해서 다음의 값들을 대입했을때:

h(x) = 1.5가 된고, 가로의 직선이 된다.
같은 가설함수에 대해서 다음의 값들을 대입했을 때:

h(x) = 0.5x가 되고, 대각선의 직선이 된다.
선형회귀
선형회귀는 다음과 같은 데이터에 가장 알맞는 직선, 즉 θ0 과 θ1 를 찾아내는 것이다.

이 때 이 직선은 학습데이터 (x,y)에 대해서 , h(x)가 y값과 최대한 가까운 값이 되는 직선이어야 한다.
목적함수
위의 개념을 공식화해보자:
이 문제의 목적은 θ0 과 θ1 를 최소화 하는것이다.
minimize θ0 θ1
즉 모든 학습데이터에 대해서 (summation),
h(x)의 값에서 y값을 뺀 값을 제곱 해 더하는 값이 최소화 되어야 한다.

위 수식에서의 m은 학습데이터의 수이고,
X와 Y의 i는 각 학습데이터의 인덱스값을 의미한다.
또한 h0(x)는 이전에 정의한 가설함수 h0(x) = θ0 + θ0x 이다.
위 수식에 붙은 1/2m은 계산을 조금 쉽게 하기 위해 곱한것이다.
(많은 머신러닝 수식에서 위와 같은 방법을 사용함)
이 수식을 다시 작성해보면,

위의 수식이 바로 비용함수이다.
이 비용함수는 Squeared Error Function이라고 불린다.
(error 함수에 제곱을 했다고 하여 위와같이 불린다)
추가자료:
비용함수 vs 목적함수
비용함수는 Error즉 h(x)값과 y값의 차이의 합을 나타내는 함수
목적함수는 위의 비용함수 Error를 통해서 무엇을 하고싶은지를 나타내는 함수
따라서 보통의 머신러닝 문제에서는 비용함수를 minimize하거나 maximize를 하는것이
목적함수가 된다.
가설함수와 비용함수
가설함수와 비용함수를 비교해보자:
- 가설함수는 x의 함수이고,
- 비용함수는 Θ1의 함수이다
다음과 같은 데이터가 있다고 하고 가설함수와 비용함수를 구해보자:
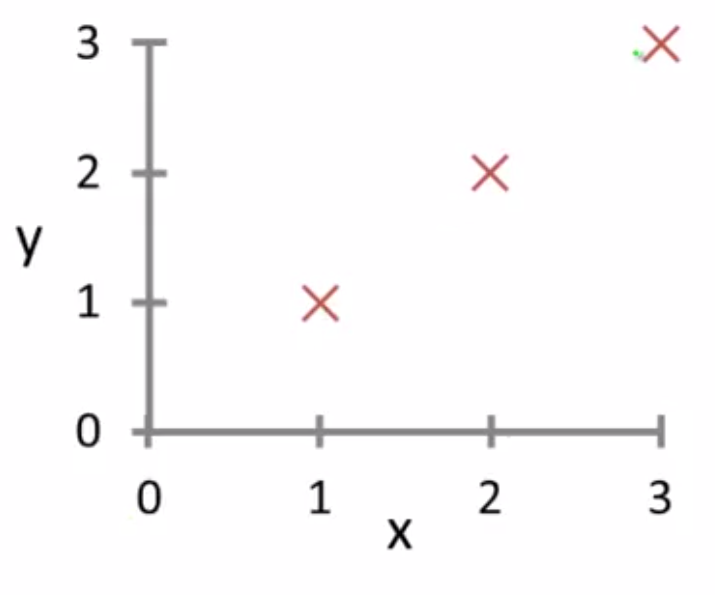
가설 1
만약 Θ1이 1이라면, 가설함수는 다음과 같이 모든 점(데이터)을 통과하는 직선이 된다:

그렇다면, Θ1가 1이라는 가설을 세우면, 비용함수는 무엇일까?

위의 수식에 대입해 계산하면, h(x) - y는 모든 값에 대해 0이 되고,
= 1/2m(0 + 0 + 0) = 0이 된다.
가설 2
그렇다면, 같은 데이터에 Θ1가 0.5라는 가설을 세우면, 비용함수는 어떻게 될까?
이번에는 데이터를 하나도 통과하지 않는 직선이 된다.

같은 수식에 대입해 계산하면, h(x) - y값은 데이터와 직선의 거리가 된다.
따라서 1/(2 * 3) * ((0.5 - 1)^2 + (1 - 2)^2 + (1.5 - 3)^2) 가 되고
이를 계산하면, 약 0.58이 된다.
가설 3
마지막으로, 같은 데이터에 Θ1가 0라는 가설을 세우면, 비용함수를 구해보자.

위의 도표에서 볼 수 있는 바와 같이, 데이터와 직선의 거리는 y값이 된다.
따라서 1/(2 * 3) * (1 + 4 + 9)가 되고, 이를 계산하면, 14/6 약 2.3333 이 된다.
위 세가지 가설에 대한 점들을 분면에 그려보면, 아래와 같은 점들이 나온다.

따라서 모든 값들에 대해 가설을 세우고, 비용을 구하면,
다음과 같은 2차 방정식같은 함수가 나오게 된다.
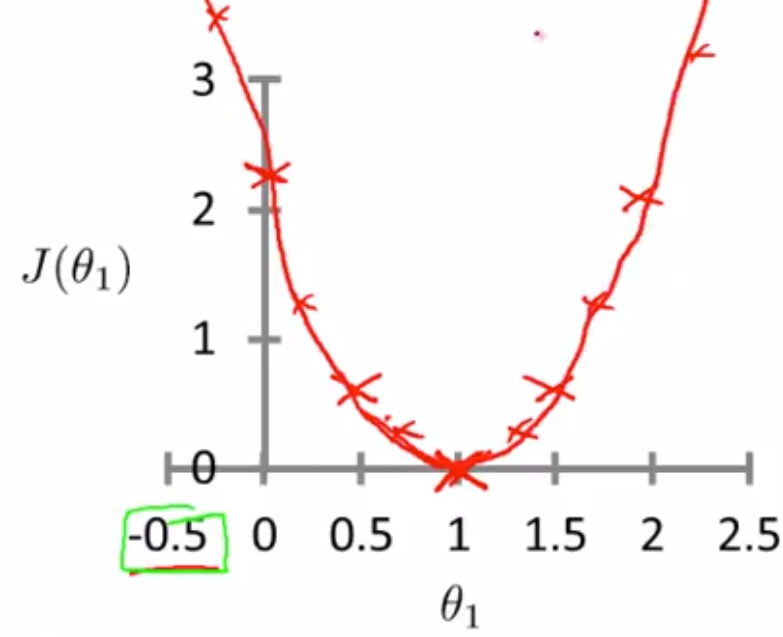
그리고 목적함수는 이것을 minimize하는 함수이고,
위의 예제에서는 Θ1가 1일때가 가장 작은 값을 가진다.
'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 머신러닝 공부 6 - 경사하강법 트릭 (0) | 2019.06.29 |
|---|---|
| 머신러닝 공부 5 - 다중 선형 회귀 (0) | 2019.06.27 |
| 머신러닝 공부 4 - 경사하강법 (0) | 2019.06.26 |
| 머신러닝 공부 2 - 단일변수 선형회귀 (0) | 2019.06.25 |
| 머신러닝 공부 1 - Intro, 지도학습, 비지도학습 (0) | 2019.06.23 |